一、图的相关概念

1.1 图的定义和术语

图的定义：图是由顶点的有穷非空集合和顶点之间的边的集合组成，通常表示为：G = (V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

无向边：若顶点V_(i )到V_(j )的边没有方向，则称这条边为无向边，用无序偶对

（V_(i ，)V_(j)）来表示。

有向边：若从顶点Vi 到V_(j)的边有方向，则称这条边为有向边，也称为弧(Arc)。用有序偶对<V_(i ，)V_(j)>来表示。V_(i)称为弧尾(Tail)或初始点，V_(j)称为弧头(Head)或终端点。

无向图: 如果图中任意两个顶点之间的边都是无向边，则称该图为无向图。

图例(G1):

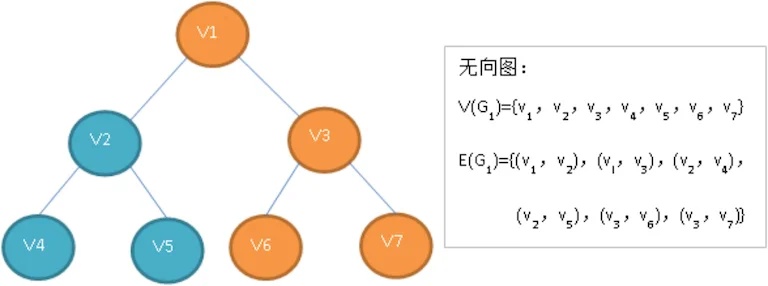
有向图: 如果图中任意顶点之间的边都是有向边，则称该图为有向图。

图例(G2):

无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。

图例(G3)

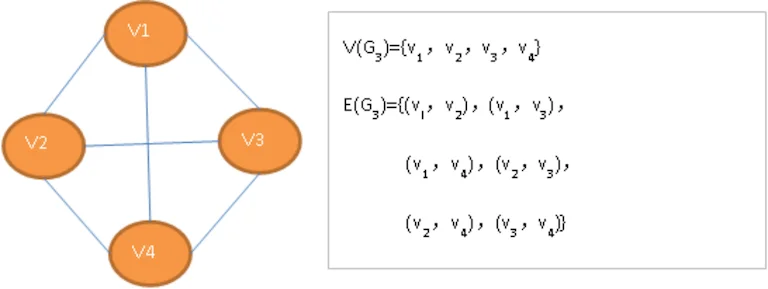
有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边。

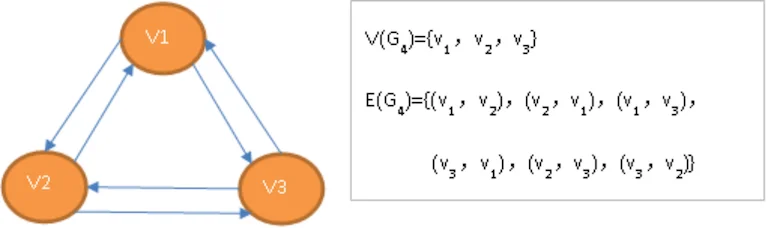
总结: 图G的顶点数n和边数e的关系

（1）

恰有n(n-1)/2条边的无向图称无向完全图(Undireet-ed Complete Graph)

（2）。

恰有n(n-1)条边的有向图称为有向完全图(Directed Complete Graph)。

注意：

。

稀疏图: 有很少条边或弧的图。

稠密图: 有很多条边或弧的图。

权: 有时图的边或弧具有与它相关的数,这种与图的边或弧相关的数叫做权。

网：带权的图通常称为网。

度：顶点的度是指和该顶点关联的边的数目。

入度：有向图中以顶点（v）为头的弧的数目，称为（v）的入度。

出度：有向图中以顶点（v）为尾的弧的数目，称为（v）的出度。

邻接点：对于无向图，同一边上的两个顶点称为邻接点。

子图: 假设两个图G=(V,E)和G1=(V1,E1),如果V1⊆V且E1⊆E则G1为G的子图

路径的长度: 路径上的边或弧的数目。

1.2 连通图相关术语

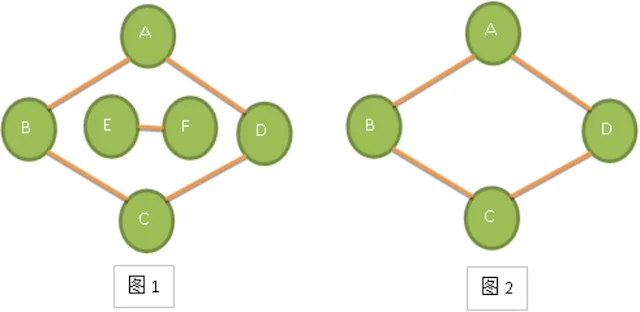
在无向图G=(V,E)中，如果从顶点v到顶点w有路径，则称v和w是相通的。如果对图中任意两个顶点Vi和Vj 属于E，则两个顶点是连通的，则称G是连通图。如下图1，它的顶点A都顶点B、C、D都是连通的，但显然顶点A与顶点E或F就无路径，因此不能算是连通图。而图2，顶点A、B、C、D相互都是连通的，所以它本身是连通图。

1.3 连通图生成树

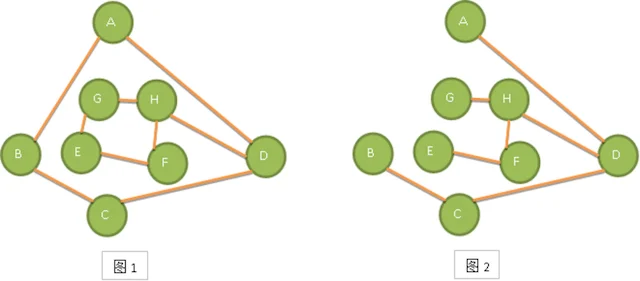
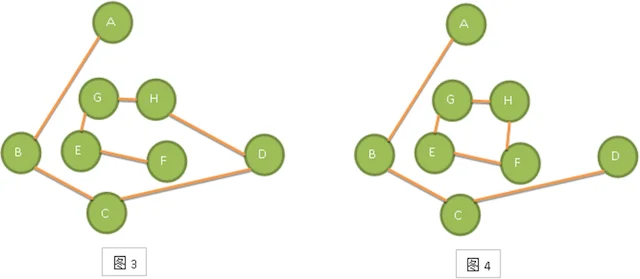
连通图的生成树是一个极小的连通子图，它含有图中全部的n个顶点，但只有足以构成一棵树的n-1条边。

比如下图的图1是一个普通图，但显然它不是生成树，当去掉两条构成环的边后，比如图2或图3，就满足n个顶点n-1条边且连通的定义了。它们都是一棵生成树。从这里也知道，如果一个图有n个顶点和小于n-1条边，则是非连通图，如果它多于n-1条边，必定构成一个环，因为这条边使得它依附的那两个顶点之间有了第二条路径。比如图2和图3，随便加哪两顶点的边都将构成环。不过有n-1条边并不一定是生成树，比如图4。

1.4 总结

图按照有无方向分为无向图和有向图。

• 无向图由顶点和边构成。
• 有向图由顶点和弧构成，弧有弧头和弧尾之分。

图按照边或弧的多少分为稀疏图和稠密图。

如果任意两个顶点之间都存在边叫完全图，有向的叫有向完全图。

与顶点相关联的边的条数叫做度，有向图顶点分为入度和出度。

图上的边或弧带权则称为网。

无向图中连通且n个顶点n-1条边叫生成树。

二、图的存储结构

2.1 邻接矩阵

图的邻接矩阵存储方式是用两个数组来表示图。

• 一个一维数组存储图中顶点信息，

• 一个二维数组（邻接矩阵）存储图中的边或弧的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

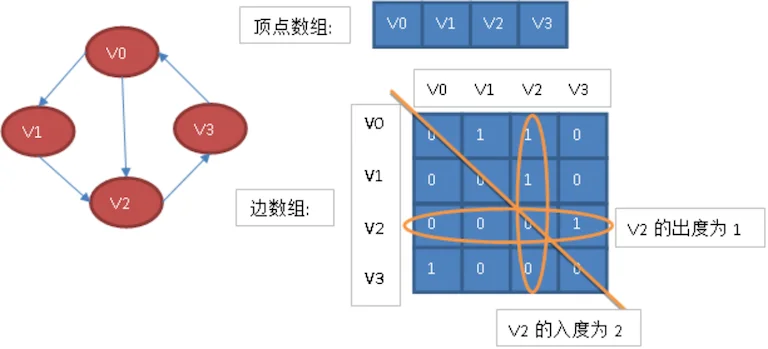
看一个实例，下图左就是一个无向图。

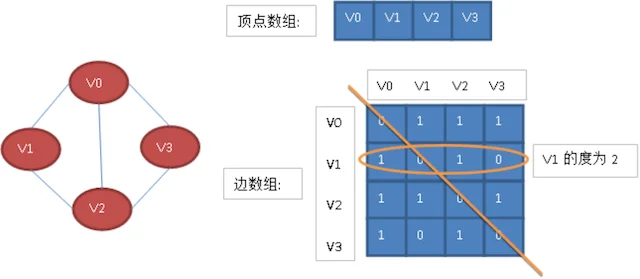
从上面可以看出，无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足a_(ij )= a_(ji)。即从矩阵的左上角到右下角的主对角线为轴，右上角的元和左下角相对应的元全都是相等的。

从这个矩阵中，很容易知道图中的信息。

• 判断任意两顶点是否有边无边；
• 某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行或（第i列）的元素之和；
• 求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点；

而有向图讲究入度和出度，顶点v2的入度为2，正好是第i列各数之和。顶点v2的出度为1，即第i行的各数之和。

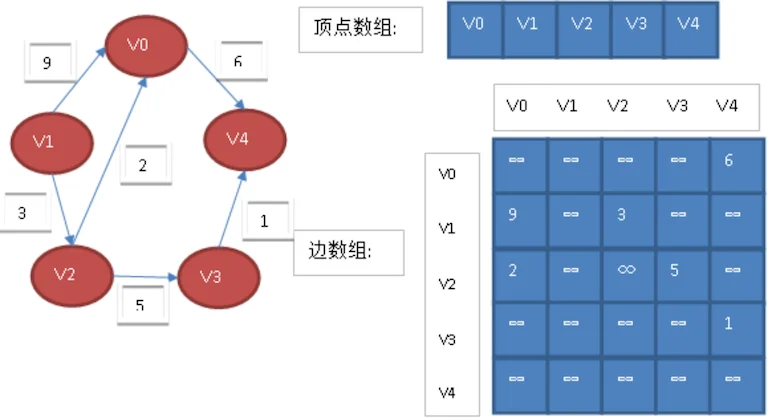
若图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

这里的wij表示(vi,vj)上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值，也就是一个不可能的极限值。下面左图就是一个有向网图，下图就是它的邻接矩阵。

2.2 邻接表

邻接矩阵是不错的一种图存储结构，但是，对于边数相对顶点较少的图，这种结构存在对存储空间的极大浪费。因此，找到一种数组与链表相结合的存储方法称为邻接表。

邻接表的存储方式是这样的：

1. 图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过，数组可以较容易的读取顶点的信息，更加方便。

2. 图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。

数据结构定义:

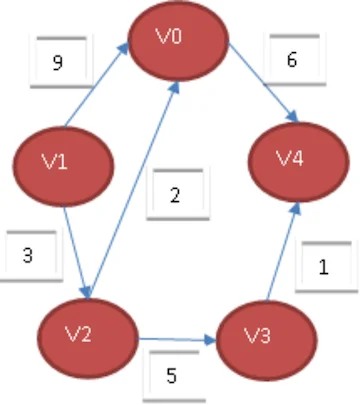
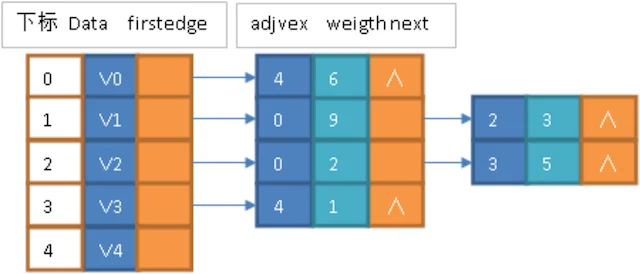
例如，下图就是一个无向图的邻接表的结构。

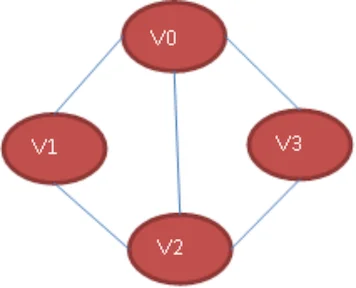
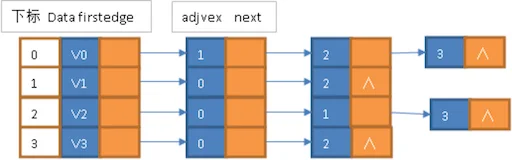
从图中可以看出，顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。

对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域，存储权值信息即可。如下图所示。

三、图的遍历

图的遍历和树的遍历类似，希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫图的遍历。

对于图的遍历来说，如何避免因回路陷入死循环，就需要科学地设计遍历方案，通常有两种遍历次序方案：深度优先遍历和广度优先遍历。

3.1 深度优先遍历

深度优先遍历，也有称为深度优先搜索，简称DFS。其实，就像是一棵树的前序遍历。

它从图中某个结点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中的所有顶点都被访问到为止。

深度优先搜索是通过栈来实现的。

下图中的数字显示了深度优先搜索顶点被访问的顺序

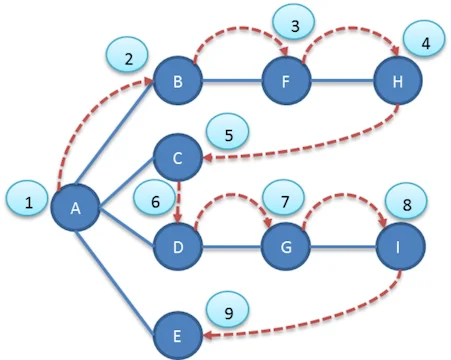
为了实现深度优先搜索，首先选择一个起始顶点并需要遵守三个规则：

• 如果可能，访问一个邻接的未访问顶点，标记它，并把它放入栈中。

• 当不能执行规则1时，如果栈不空，就从栈中弹出一个顶点。

• 如果不能执行规则1和规则2，就完成了整个搜索过程。

3.2 广度优先遍历

广度优先遍历，又称为广度优先搜索，简称BFS。图的广度优先遍历就类似于树的层序遍历了。

在深度优先搜索中，算法表现得好像要尽快地远离起始点似的。相反，在广度优先搜索中，算法好像要尽可能地靠近起始点。。

下面图中的数字显示了广度优先搜索顶点被访问的顺序。

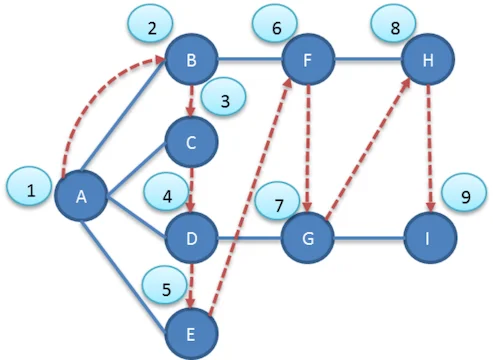
实现广度优先搜索，也要遵守三个规则：

• 访问下一个未来访问的邻接点，这个顶点必须是当前顶点的邻接点，标记它，并把它插入到队列中。

• 如果因为已经没有未访问顶点而不能执行规则1时，那么从队列头取一个顶点，并使其成为当前顶点。

• 如果因为队列为空而不能执行规则2，则搜索结束。

四、最小生成树

• 相关概念

生成树：一个连通图的生成树是它的极小连通子图，在n个顶点的情形下，有n-1条边。生成树是对连通图而言的，是连同图的极小连通子图，包含图中的所有顶点，有且仅有n-1条边。

最小生成树：在图论中，常常将树定义为一个无回路连通图。对于一个带权的无向连通图，其每个生成树所有边上的权值之和可能不同，我们把所有边上权值之和最小的生成树称为图的最小生成树。

• 案例（造价最优问题就是一个最小生成树问题）

铺设煤气管道问题（图形结构）假设要在某个城市的n个居民区之间铺设煤气管道，则在这n个居民区之间只要铺设n-1条管道即可。假设任意两个居民区之间都可以架设管道，管道铺设方案。在众多可选边中，如何选择n-1条边，使总代价最小？这就是求该网络最小生成树问题。

• 普里姆（Prim）算法

  • 基本思想：设G=(V, E)是具有n个顶点的连通网，T=(U, TE)是G的最小生成树，T的初始状态为U={u0}（u0∈V），TE={}，重复执行下述操作：在所有u∈U，v∈V-U的边中找一条代价最小的边(u, v)并入集合TE，同时v并入U，直至U=V。即：

    • 从连通网络 G = { V, E }中的某一顶点 u0 出发，选择与它关联的具有最小权值的边(u0, v)，将其顶点加入到生成树的顶点集合U中。

    • 以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(u, v),把它的顶点加入到集合U中。如此继续下去，直到网络中的所有顶点都加入到生成树顶点集合U中为止。

此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

Prim算法的核心:始终保持TE中的边集构成一棵生成树。

• 示例

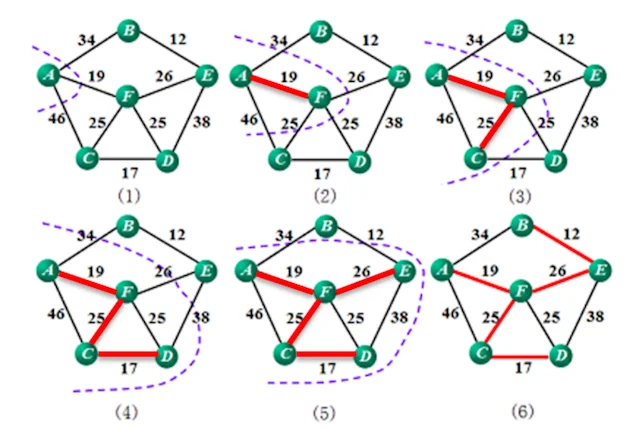
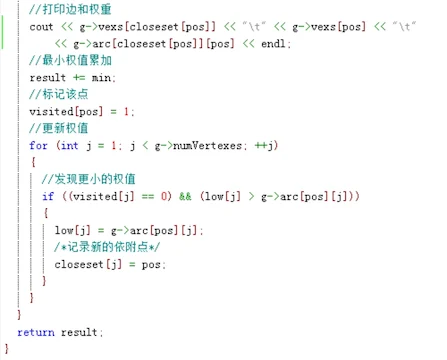
算法实现:

• 克鲁斯卡尔（Kruskal）算法

  • 基本思想：设无向连通网为G＝(V, E)，令G的最小生成树为T＝(U, TE)，其初态为U＝V，TE＝{ }，然后，按照边的权值由小到大的顺序，考察G的边集E中的各条边。若被考察的边的两个顶点属于T的两个不同的连通分量，则将此边作为最小生成树的边加入到T中，同时把两个连通分量连接为一个连通分量；若被考察边的两个顶点属于同一个连通分量，则舍去此边，以免造成回路，如此下去，当T中的连通分量个数为1时，此连通分量便为G的一棵最小生成树。

  • 示例

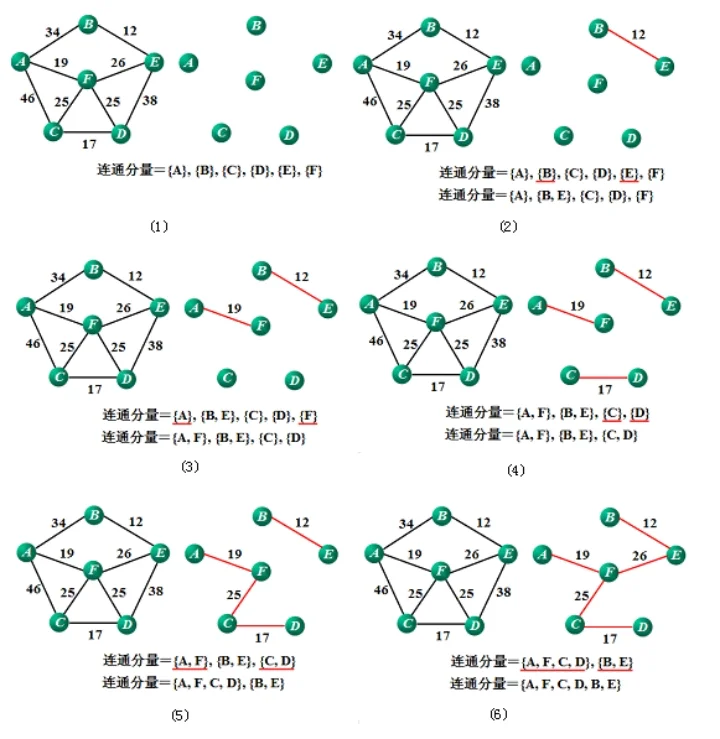
两种算法总结:

prim算法适合稠密图，其时间复杂度为O(n²)，其时间复杂度与边得数目无关，而kruskal算法的时间复杂度为O(nlogn)跟边的数目有关，适合稀疏图。

五、最短路径

基本概念

最短路径：从图中某一顶点（源点）到达另一顶点（终点）找到一条路径，沿此路径上各边的权值总和（称为路径长度）达到最小。
单源最短路径：已知有向带权图(简称有向网)G=(V，E)，找出从某个源点s∈V到V中其余各顶点的最短路径。

习惯上称路径开始顶点为源点，路径的最后一个顶点为终点。

最短路径的最优子结构性质

该性质描述为：如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径，k和s是这条路径上的一个中间顶点，那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。

假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径，则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离，那么必定存在另一条从k到s的最短路径P'(k,s)，那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。(如图)

• 迪杰斯特拉(Dijkstra)算法

由上述性质可知，如果存在一条从i到j的最短路径(Vi.....Vk,Vj)，Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径，Dijkstra就提出了以最短路径长度递增，逐次生成最短路径的算法。譬如对于源顶点V0，首先选择其直接相邻的顶点中长度最短的顶点Vi，那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根据这种思路，假设存在G=<V,E>，源顶点为V0，U={V0},dist[i]记录V0到i的最短距离，path[i]记录从V0到i路径上的i前面的一个顶点。

• 从V-U中选择使dist[i]值最小的顶点i，将i加入到U中；

• 更新与i直接相邻顶点的dist值。

(dist[j]=min{dist[j],dist[i]+matrix[i][j]})

• 直到U=V，停止。

 

• 案例

交通网络可以画成带权的图，图中顶点表示城市，边代表城市间的公路，边上的权表示公路的长度。对于这样的交通网络常常提出这样的问题：两地之间是否有公路可通？在有几条路可通的情况下，哪一条路最短？以上提出的问题就是在带权图中求最短路径问题，此时路径的长度不是路径上边的数目，而是路径上的边所带权值的总和。

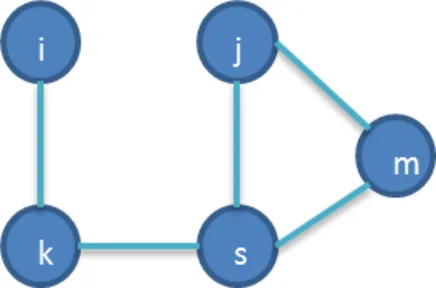
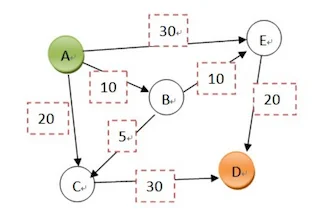
在下面图中找出 A 城到 D 城最近的一条公路。

本次用于分析的拓扑图如下：(A为起点，D为终点，边上的数字为权值)

六、Prim算法和Dijkstra算法的异同

主要有以下几点：

• 1

Prim是计算最小生成树的算法，比如为N个村庄修路，怎么修花销最少。

Dijkstra是计算最短路径的算法，比如从a村庄走到其他任意村庄的距离。

• 2

Prim算法中有一个统计总len的变量，每次都要把到下一点的距离加到len中；

Dijkstra算法中却没有，只需要把到下一点的距离加到cls数组中即可；

• 3

Prim算法的更新操作更新的low是已访问集合到未访问集合中各点的距离；

Dijkstra算法的更新操作更新的dist是源点到未访问集合中各点的距离，已经访问过的相当于已经找到源点到它的最短距离了；