算法实战
二叉树相关的算法实战基本都是与递归相关的,因为它实在是太适合用分治算法了!
(简单)二叉查找树的范围和
本题来自LeetCode:938. 二叉搜索树的范围和
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和。
示例 1:
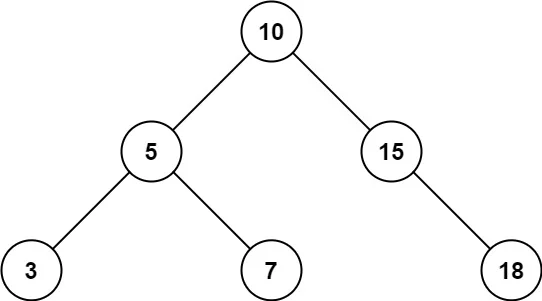
输入:root = [10,5,15,3,7,null,18], low = 7, high = 15 (注意力扣上的输入案例写的是层序序列,含空节点) 输出:32
示例 2:
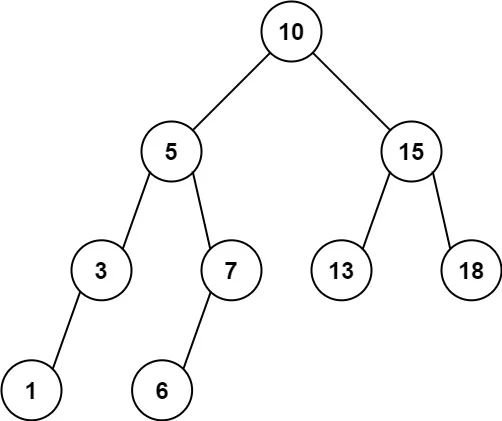
输入:root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 输出:23
这道题其实就是考察我们对于二叉查找树的理解,利用二叉查找树的性质,这道题其实很简单,只需要通过递归分治就可以解决了。
代码如下:
int rangeSumBST(struct TreeNode* root, int low, int high){
if(root == NULL) return 0;
if(root->val > high) //如果最大的值都比当前结点值小,那么肯定在左边才能找到
return rangeSumBST(root->left, low, high);
else if(root->val < low) //如果最小值都比当前结点大,那么肯定在右边才能找到
return rangeSumBST(root->right, low, high);
else
//这种情况肯定是在范围内了,将当前结点值加上左右的,再返回
return root->val + rangeSumBST(root->right, low, high) + rangeSumBST(root->left, low, high);
}这种问题比较简单,直接四行就解决了。
(中等)重建二叉树
本题来自LeetCode:剑指 Offer 07. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
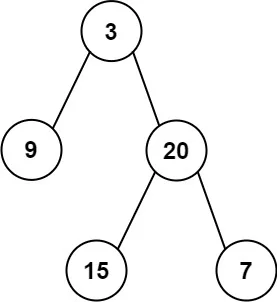
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
实际上这道题就是我们前面练习题的思路,现在给到我们的是前序和中序遍历的结果,我们只需要像之前一样逐步推导即可。
在中序遍历序列中找到根节点的位置后,这个问题就很好解决了,大致思路如下:
- 由于前序遍历首元素为根节点值,首先可以得到根节点值。
- 在中序遍历序列中通过根节点的值,寻找根节点的位置。
- 将左右两边的序列分割开来,并重构为根节点的左右子树。(递归分治)
- 在新的序列中,重复上述步骤,通过前序遍历再次找到当前子树的根节点,再次进行分割。
- 直到分割到仅剩下一个结点时,开始回溯,从而完成整棵二叉树的重建。
解题代码如下:
struct TreeNode * createNode(int val){ //这个就是单纯拿来创建结点的函数
struct TreeNode * node = malloc(sizeof(struct TreeNode));
node->left = node->right = NULL;
node->val = val;
return node;
}
//核心递归分治实现
struct TreeNode* buildTreeCore(int * preorder, int * inorder, int start, int end, int index){
if(start > end) return NULL; //如果都超出范围了,肯定不行
if(start == end) return createNode(preorder[index]); //如果已经到头了,那么直接创建结点返回即可
struct TreeNode * node = createNode(preorder[index]); //先从前序遍历中找到当前子树的根结点值,然后创建对应的结点
int pos = 0;
while (inorder[pos] != preorder[index]) pos++; //找到中序的对应位置,从这个位置开始左右划分
node->left = buildTreeCore(preorder, inorder, start, pos - 1, index+1);
//当前结点的左子树按照同样的方式建立
//因为前序遍历的下一个结点就是左子树的根结点,所以说这里给index+1
node->right = buildTreeCore(preorder, inorder, pos+1, end, index+(pos-start)+1);
//当前结点的右子树按照同样的方式建立
//最后一个index需要先跳过左子树的所有结点,才是右子树的根结点,所以说这里加了个pos-start,就是中序划分出来,左边有多少就减去多少
return node; //向上一级返回当前结点
}
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
return buildTreeCore(preorder, inorder, 0, preorderSize - 1, 0);
//这里传入了前序和中序序列,并且通过start和end指定当前中序序列的处理范围,最后的一个index是前序遍历的对应头结点位置
}(中等)验证二叉搜索树
本题来自LeetCode:98. 验证二叉搜索树(先说,这题老六行为过多,全站通过率只有36.5%,但是题目本身很简单)
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。 节点的右子树只包含 大于 当前节点的数。 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3] 输出:true
示例 2:
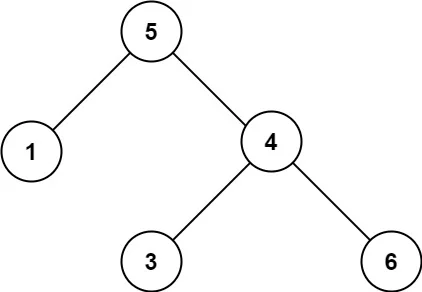
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
这种题看起来好像还挺简单的,我们可以很快地写出代码:
bool isValidBST(struct TreeNode* root){
if(root == NULL) return true; //到头了就直接返回真
if(root->left != NULL && root->left->val >= root->val) return false; //如果左边不是空,并且左边还比当前结点值小的话,那肯定不是了
if(root->right != NULL && root->right->val <= root->val) return false; //同上
return isValidBST(root->left) && isValidBST(root->right); //接着向下走继续判断左右两边子树,必须同时为真才是真
}然后直接上力扣测试,嗯,没问题,提交,这把必过!于是光速打脸:
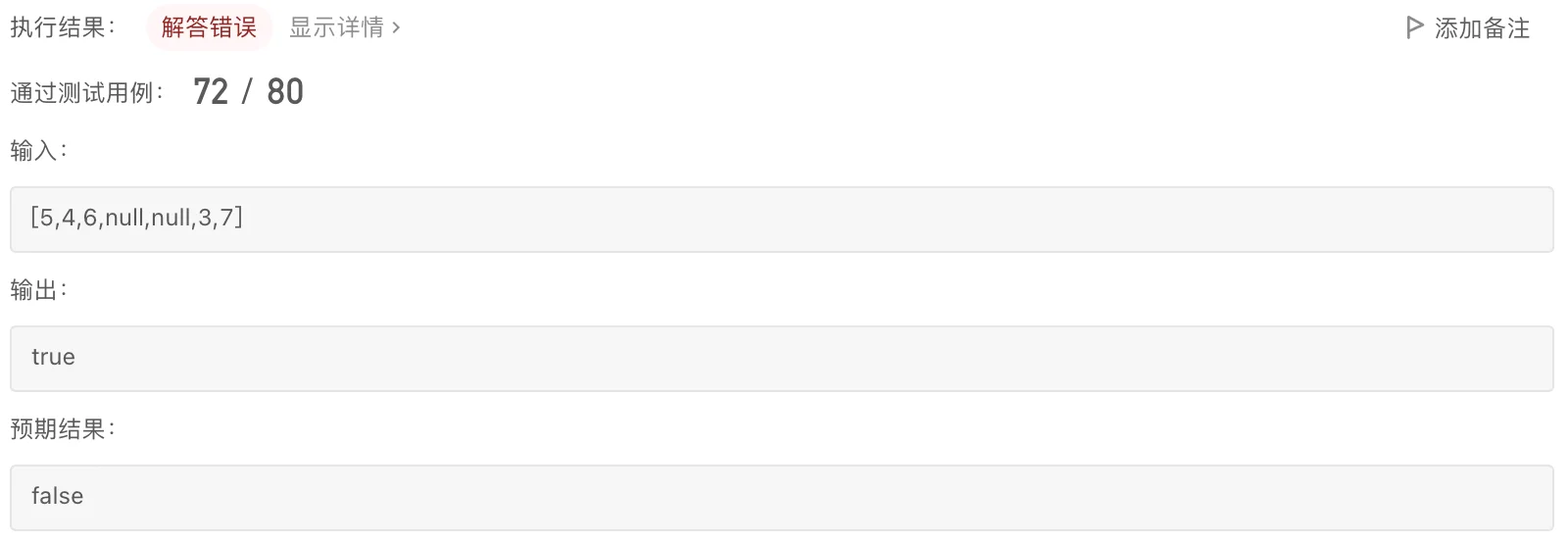
不可能啊,我们的逻辑判断没有问题的,我们的算法不可能被卡的啊?(这跟我当时打ACM一样的感觉,我这天衣无缝的算法不可能错的啊,哪个老六测试用例给我卡了)这其实是因为我们没有考虑到右子树中左子树比根结点值还要小的情况:
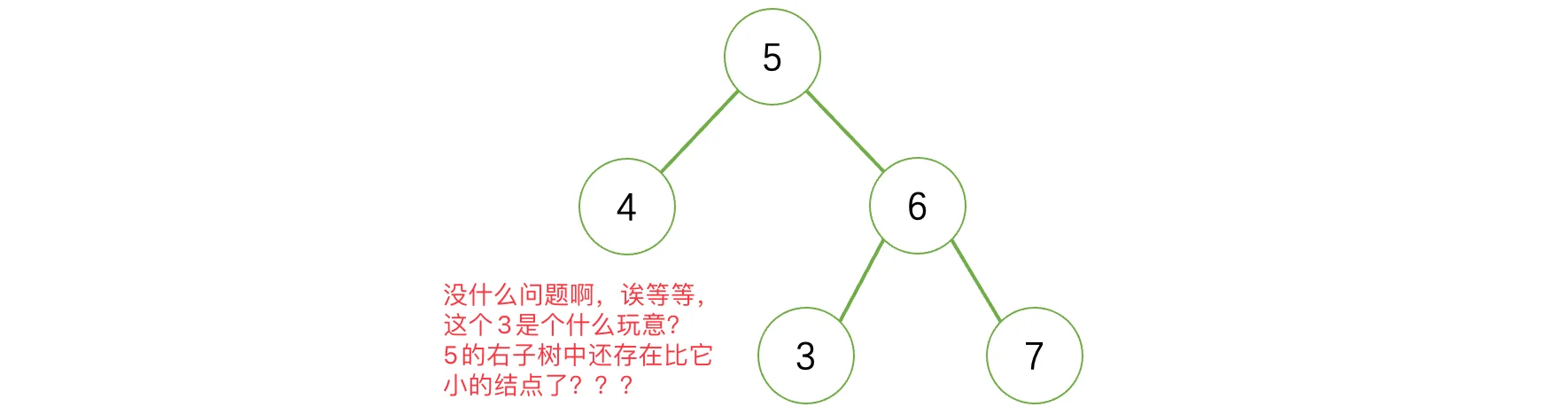
虽然这样错的很明显,但是按照我们上面的算法,这种情况确实也会算作真。所以说我们需要改进一下,对其上界和下界进行限定,不允许出现这种低级问题:
bool isValid(struct TreeNode* root, long min, long max){ //这里上界和下界用long表示,因为它的范围给到整个int,真是个老六
if(root == NULL) return true;
//这里还需要判断是否正常高于下界
if(root->left != NULL && (root->left->val >= root->val || root->left->val <= min))
return false;
//这里还需判断一下是否正常低于上界
if(root->right != NULL && (root->right->val <= root->val || root->right->val >= max))
return false;
return isValid(root->left, min, root->val) && isValid(root->right, root->val, max);
//注意往左走更新上界,往右走更新下界
}
bool isValidBST(struct TreeNode* root){
return isValid(root, -2147483649, 2147483648); //下界刚好比int少1,上界刚好比int多1
}这样就没问题了。
(中等)求根到叶数字之和
本题来自LeetCode:129. 求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字 13 因此,数字总和 = 12 + 13 = 25
示例 2:
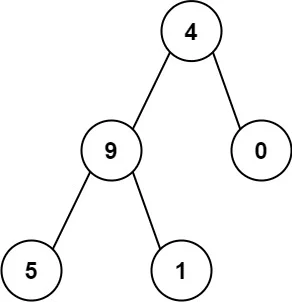
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此,数字总和 = 495 + 491 + 40 = 1026
这道题其实也比较简单,直接从上向下传递当前路径上已经组装好的值即可,到底时返回最终的组装结果:
int sumNumbersImpl(struct TreeNode * root, int parent){
if(root == NULL) return 0; //如果到头了,直接返回0
int sum = root->val + parent * 10; //因为是依次向后拼接,所以说直接将之前的值x10然后加上当前值即可
if(!root->left && !root->right) //如果是叶子结点,那么直接返回结果
return sum;
//否则按照同样的方式将左右的结果加起来
return sumNumbersImpl(root->left, sum) + sumNumbersImpl(root->right, sum);
}
int sumNumbers(struct TreeNode* root){
return sumNumbersImpl(root, 0);
}(困难)结点之和的最大路径
本题来自LeetCode:剑指 Offer II 051. 节点之和最大的路径(这是一道Hard难度的题目,但是其实还好)
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给定一个二叉树的根节点 root ,返回其 最大路径和,即所有路径上节点值之和的最大值。
示例 1:
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
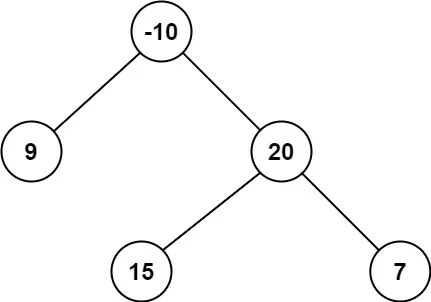
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
首先,我们要知道,路径有很多种可能,要么从上面下来,要么从左边上来往右边走,要么只走右边,要么只走左边...我们需要寻找一个比较好的方法在这么多种可能性之间选择出最好的那一个。
int result = -2147483648; //使用一个全局变量来存储一下当前的最大值
int max(int a, int b){ //不想多说了
return a > b ? a : b;
}
int maxValue(struct TreeNode* root){
if(root == NULL) return 0;
//先把左右两边走或是不走的情况计算一下,取出值最大的情况
int leftMax = max(maxValue(root->left), 0);
int rightMax = max(maxValue(root->right), 0);
//因为要么只走左边,要么只走右边,要么左右都走,所以说我们计算一下最大情况下的结果
int maxTmp = leftMax + rightMax + root->val;
result = max(maxTmp, result); //更新一下最大值
//然后就是从上面下来的情况了,从上面下来要么左要么右,此时我们只需要返回左右最大的一个就行了
return max(leftMax, rightMax) + root->val; //注意还要加上当前结点的值,因为肯定要经过当前结点
}
int maxPathSum(struct TreeNode* root){
maxValue(root);
return result; //最后返回完事之后最终得到的最大值
}这样,我们就成功解决了这种问题。