堆和优先级队列

前面我们在讲解哈夫曼树时了解了优先级队列，它提供一种可插队的机制，允许权值大的结点排到前面去，但是出队顺序还是从队首依次出队。我们通过对前面的队列数据结构的插入操作进行改造，实现了优先级队列。

这节课我们接着来了解一下堆（Heap）它同样可以实现优先级队列。

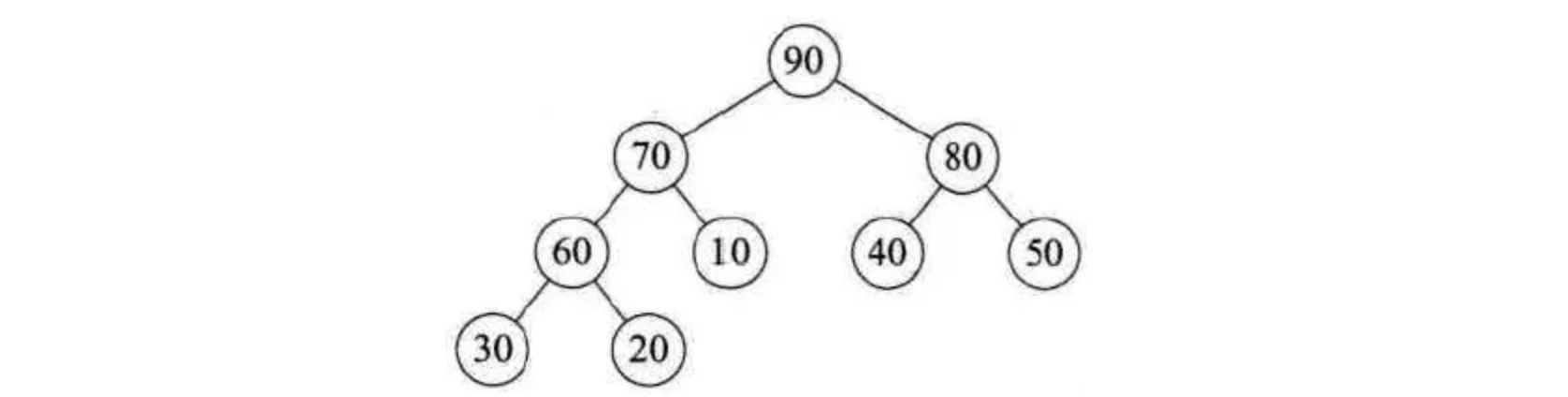
首先必须是一棵完全二叉树，树中父亲都比孩子小的我们称为小根堆（小顶堆），树中父亲都比孩子大则是大根堆（注意不要跟二叉查找树搞混了，二叉查找树是左小右大，而堆只要是孩子一定小或者大），它是一颗具有特殊性质的完全二叉树。比如下面就是一个典型的大根堆：

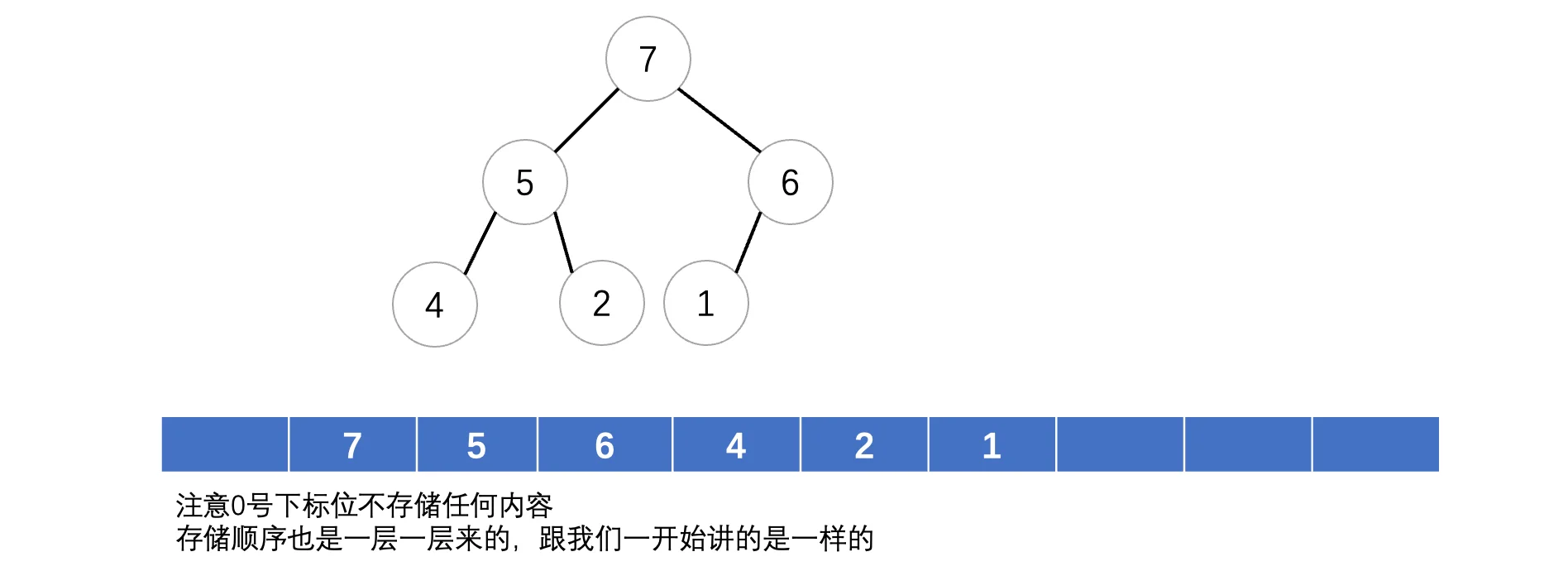
因为完全二叉树比较适合使用数组才存储（因为是按序的）所以说一般堆都是以数组形式存放：

那么它是怎么运作的呢？比如现在我们想要往堆中插入一个新的元素8，那么：

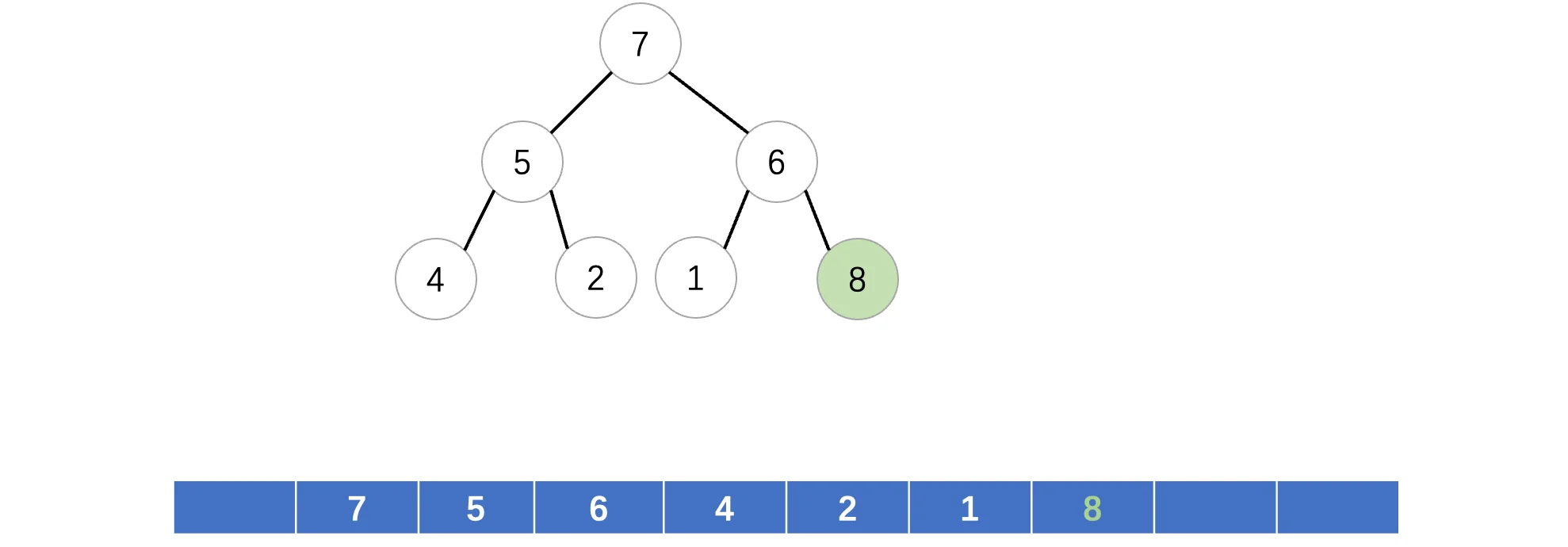
因为是一棵完全二叉树，那么必须按照顺序，继续在当前这一行从左往右插入新的结点，其实就相当于在数组的后面继续加一个新的进来，是一样的。但是因为要满足大顶堆的性质，所以此时8加入之后，破坏了规则，我们需要进行对应的调整（堆化），很简单，我们只需要将其与父结点交换即可：

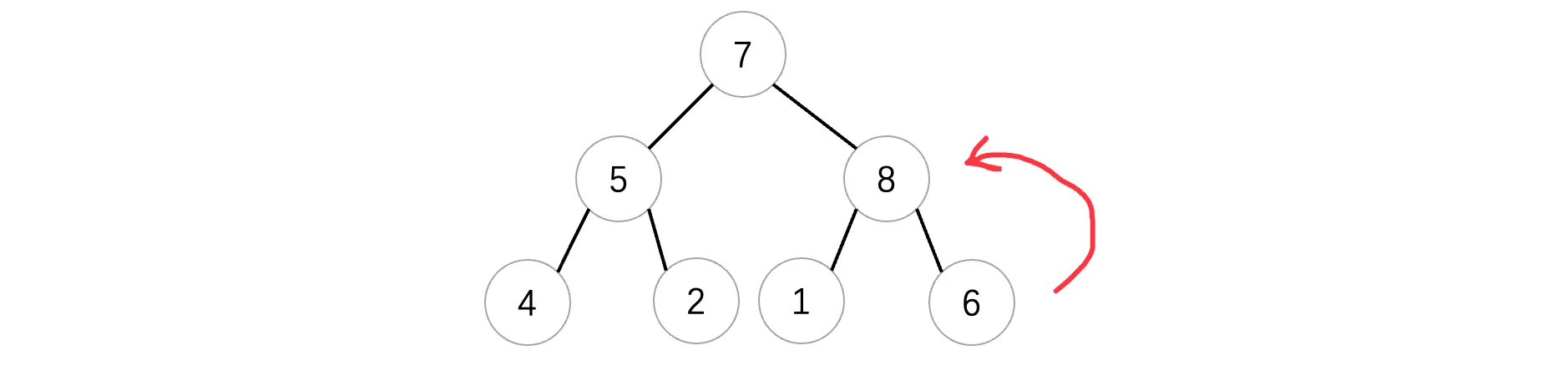
同样的，数组的形式的话，我们就行先计算出它的父结点，然后进行交换即可：

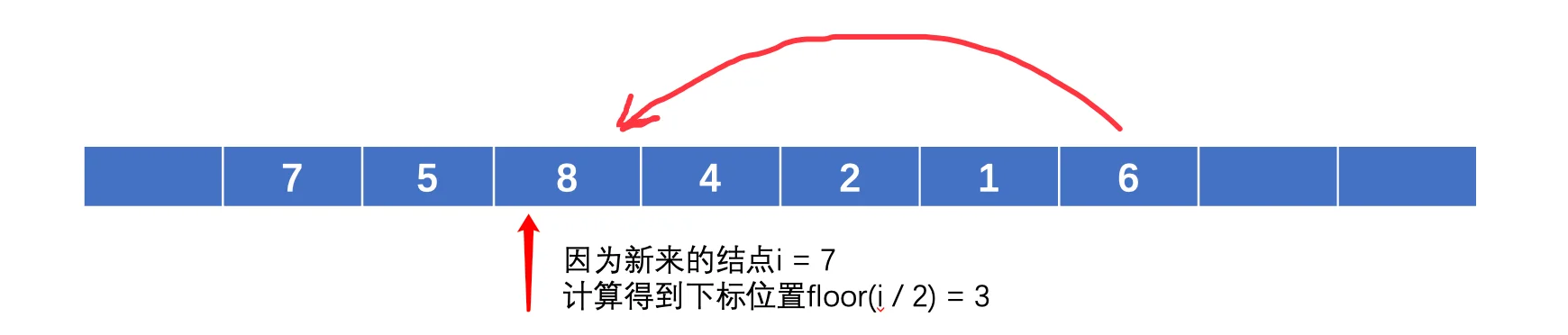
当然，还没完，我们还需要继续向上比较，直到稳定为止，此时7依然是小于8的，所以说需要继续交换：

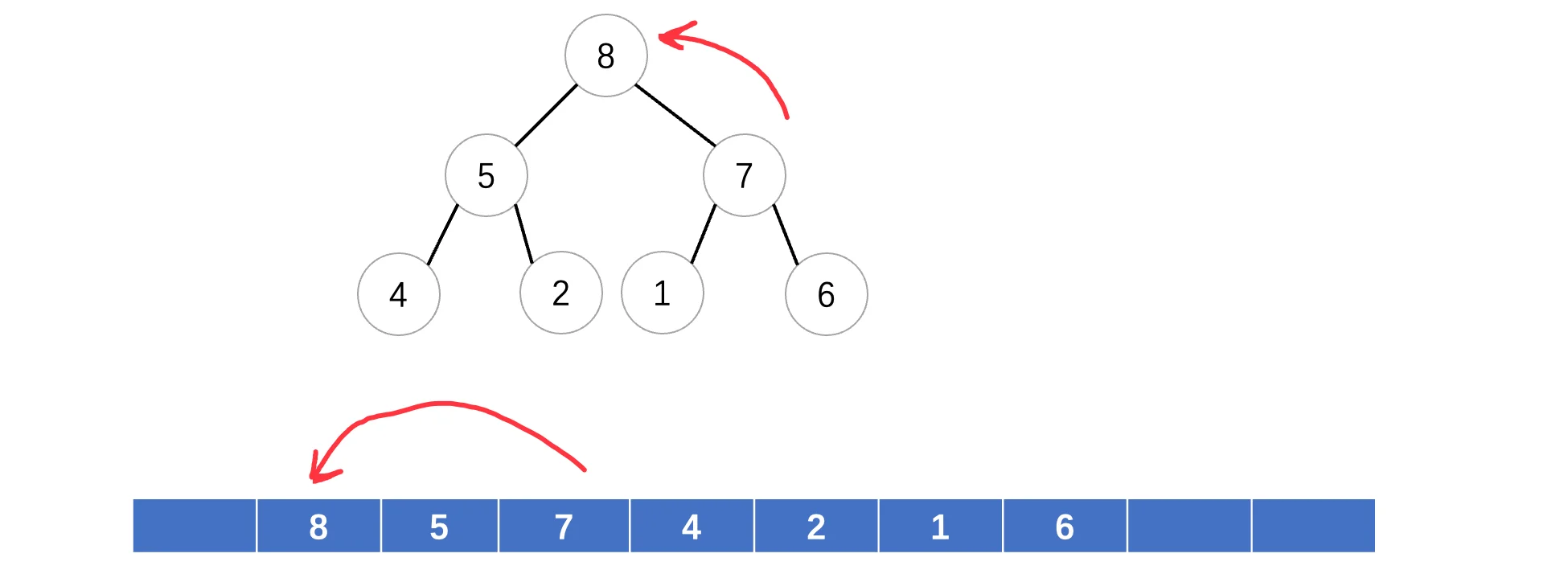
现在满足性质了，堆化结束，可以看到最大的元素被排到了最前面，这不就是我们前面的优先级队列吗。

现在我们来试试看删除队首元素，也就相当于出队操作，删除最顶上的元素：

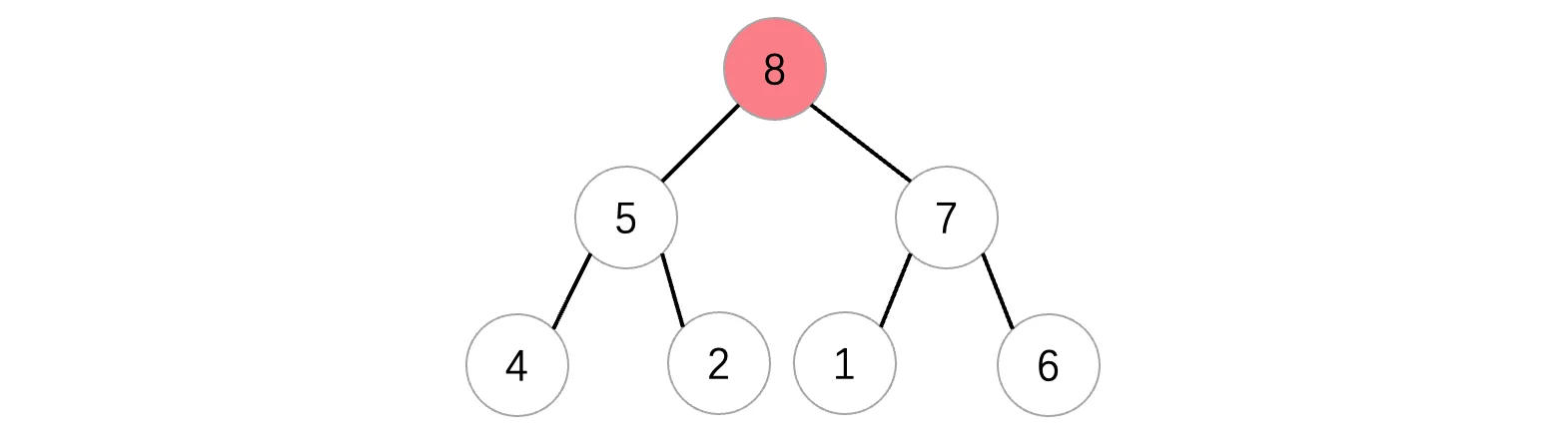
现在需要删除最顶上的元素但是我们需要保证删除之后依然是一棵完全二叉树，所以说我们先把排在最后面的拿上来顶替一下：

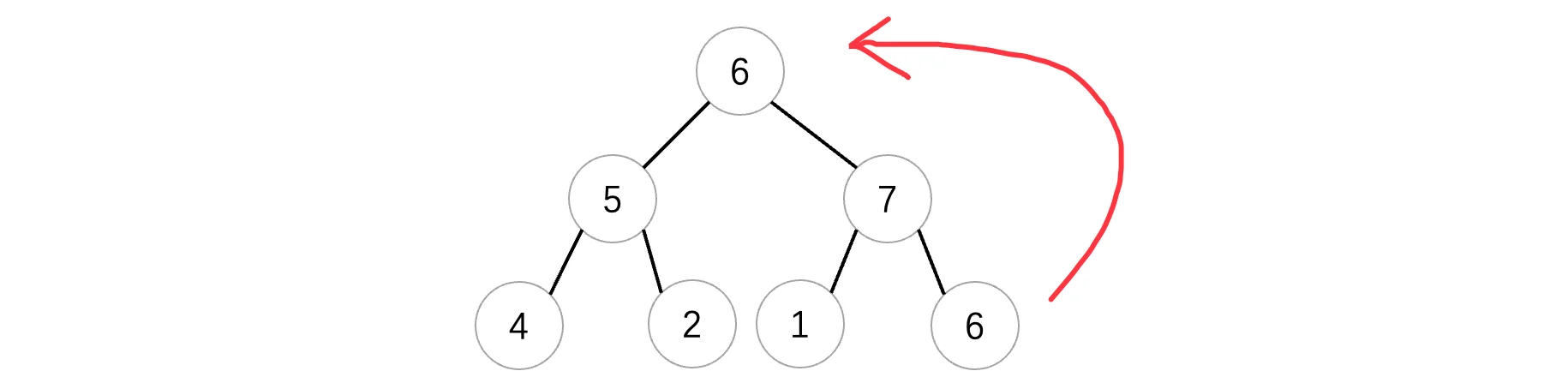
接着我们需要按照与插入相反的方向，从上往下进行堆化操作，规则是一样的，遇到大的就交换，直到不是为止：

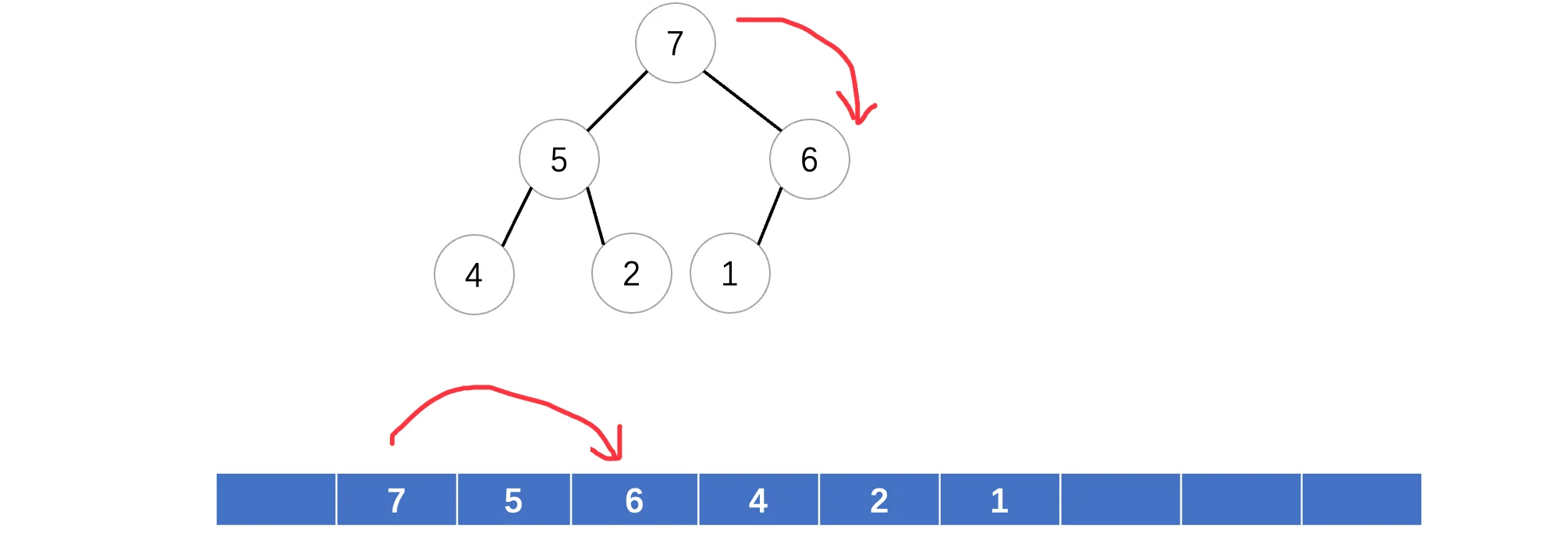
这样，我们发现，即使完成了出队操作，依然是最大的元素排在队首，并且整棵树依然是一棵完全二叉树。

按照上面的操作，我们来编写一下代码吧，这里还是以大顶堆为例：

typedef int E;
typedef struct MaxHeap {
    E * arr;
    int size;
    int capacity;
} * Heap;

_Bool initHeap(Heap heap){   //初始化都是老套路了，不多说了
    heap->size = 0;
    heap->capacity = 10;
    heap->arr = malloc(sizeof (E) * heap->capacity);
    return heap->arr != NULL;
}

int main(){
    struct MaxHeap heap;
    initHeap(&heap);
}

接着就是插入操作，首先还是需要判断是否已满：

_Bool insert(Heap heap, E element){
    if(heap->size == heap->capacity) return 0;   //满了就不处理了，主要懒得写扩容了
    int index = ++heap->size;   //先计算出要插入的位置，注意要先自增，因为是从1开始的
    //然后开始向上堆化，直到符合规则为止
    while (index > 1 && element > heap->arr[index / 2]) {
        heap->arr[index] = heap->arr[index / 2];
        index /= 2;
    }
    //现在得到的index就是最终的位置了
    heap->arr[index] = element;
    return 1;
}

我们来测试一下吧：

void printHeap(Heap heap){
    for (int i = 1; i <= heap->size; ++i)
        printf("%d ", heap->arr[i]);
}

int main(){
    struct MaxHeap heap;
    initHeap(&heap);
    insert(&heap, 5);
    insert(&heap, 2);
    insert(&heap, 3);
    insert(&heap, 7);
    insert(&heap, 6);

    printHeap(&heap);
}

最后结果为：

插入完成之后，我们接着来写一下删除操作，删除操作实际上就是出队的操作：

E delete(Heap heap){
    E max = heap->arr[1], e = heap->arr[heap->size--];
    int index = 1;
    while (index * 2 <= heap->size) {   //跟上面一样，开找，只不过是从上往下找
        int child = index * 2;   //先找到左孩子
        //看看右孩子和左孩子哪个大，先选一个大的出来
        if(child < heap->size && heap->arr[child] < heap->arr[child + 1])
            child += 1;
        if(e >= heap->arr[child]) break;   //如果子结点都不大于新结点，那么说明就是这个位置，结束就行了
        else heap->arr[index] = heap->arr[child];  //否则直接堆化，换上去
        index = child;   //最后更新一下index到下面去
    }
    heap->arr[index] = e;   //找到合适位置后，放进去就行了
    return max;
}

最后我们来测试一下吧：

int main(){
    struct MaxHeap heap;
    initHeap(&heap);
    ...
    for (int i = 0; i < 5; ++i) {
        printf("%d ", delete(&heap));
    }
}

可以看到结果就是优先级队列的出队结果，这样，我们就编写好了大顶堆的插入和删除操作了。

当然，堆在排序上也有着非常方便的地方，在后面的排序算法篇中，我们还会再次说起它。

至此，有关树形结构篇的内容，我们就全部讲解完毕了，请务必认真掌握前面的二叉树和高级二叉树结构，这些都是重点内容，下一章我们将继续探讨散列表。

堆和优先级队列 ​

堆和优先级队列