二叉搜索树（Binary Search Tree, BST）

还记得我们开篇讲到的二分搜索算法吗？通过不断缩小查找范围，最终我们可以以很高的效率找到有序数组中的目标位置。而二叉查找树则利用了类似的思想，我们可以借助其来像二分搜索那样快速查找。

二叉查找树也叫二叉搜索树或是二叉排序树，它具有一定的规则：

左子树中所有结点的值，均小于其根结点的值。
右子树中所有结点的值，均大于其根结点的值。
二叉搜索树的子树也是二叉搜索树。

一棵二叉搜索树长这样：

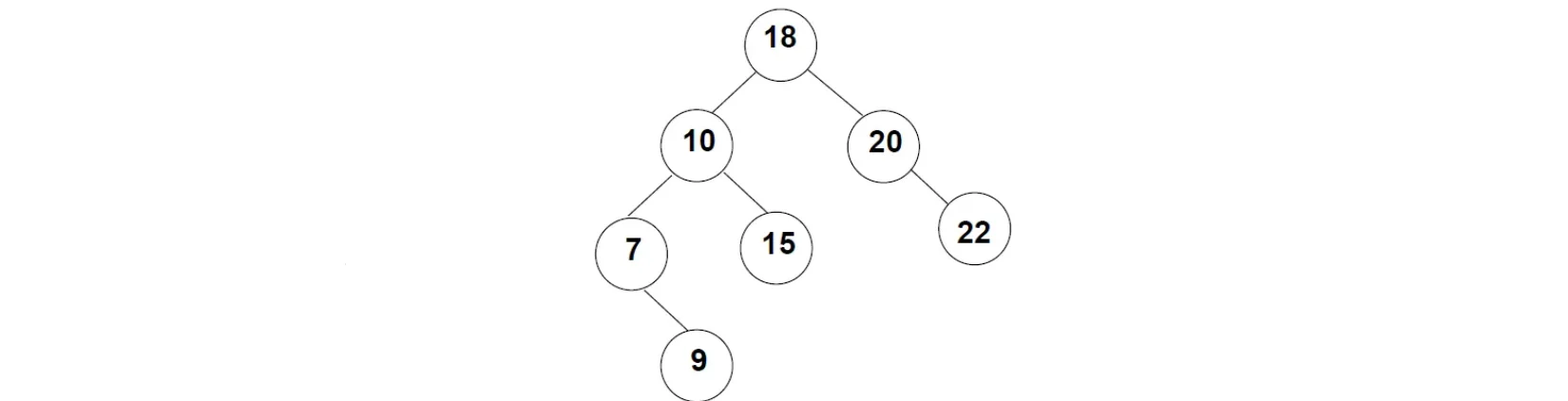
这棵树的根结点为18，而其根结点左边子树的根结点为10，包括后续结点，都是满足上述要求的。二叉查找树满足左边一定比当前结点小，右边一定比当前结点大的规则，比如我们现在需要在这颗树种查找值为15的结点：

从根结点18开始，因为15小于18，所以从左边开始找。
接着来到10，发现10比15小，所以继续往右边走。
来到15，成功找到。

实际上，我们在对普通二叉树进行搜索时，可能需要挨个进行查看比较，而有了二叉搜索树，查找效率就大大提升了，它就像我们前面的二分搜索那样。

因为二叉搜索树要求比较严格，所以我们在插入结点时需要遵循一些规律，这里我们来尝试编写一下：

#include <stdio.h>
#include <stdlib.h>

typedef int E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
} * Node;

Node createNode(E element){
    Node node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    return node;
}

int main() {
    
}

我们就以上面这颗二叉查找树为例，现在我们想要依次插入这些结点，我们需要编写一个特殊的插入操作，这里需要注意一下，二叉查找树不能插入重复元素，如果出现重复直接忽略：

Node insert(Node root, E element){
    if(root){
        if(root->element > element)    //如果插入结点值小于当前结点，那么说明应该放到左边去
            root->left = insert(root->left, element);
        else if(root->element < element)    //如果插入结点值大于当前结点，那么说明应该放到右边去
            root->right = insert(root->right, element);
    } else {   //当结点为空时，说明已经找到插入的位置了，创建对应结点
        root = createNode(element);
    }
    return root;   //返回当前结点
}

这样我们就可以通过不断插入创建一棵二叉查找树了：

void inOrder(Node root){
    if(root == NULL) return;
    inOrder(root->left);
    printf("%d ", root->element);
    inOrder(root->right);
}

int main() {
    Node root = insert(NULL, 18);   //插入后，得到根结点
    inOrder(root);   //用中序遍历查看一下结果
}

我们按照顺序来，首先是根结点的左右孩子，分别是10和20，那么这里我们就依次插入一下：

int main() {
    Node root = insert(NULL, 18);   //插入后，得到根结点
    insert(root, 10);
    insert(root, 20);
    inOrder(root);
}

可以看到中序结果为：

比18小的结点在左边，大的在右边，满足二叉查找树的性质。接着是7、15、22：

最后再插入9就是我们上面的这棵二叉查找树了。当然我们直接写成控制台扫描的形式，就更方便了：

int main() {
    Node root = NULL;
    while (1) {
        E element;
        scanf("%d", &element);
        root = insert(root, element);
        inOrder(root);
        putchar('\n');
    }
}

那么插入写好之后，我们怎么找到对应的结点呢？实际上也是按照规律来就行了：

Node find(Node root, E target){
    while (root) {
        if(root->element > target)    //如果要找的值比当前结点小，说明肯定在左边
            root = root->left;
        else if(root->element < target)   //如果要找的值比当前结点大，说明肯定在右边
            root = root->right;
        else
            return root;   //等于的话，说明找到了，就直接返回
    }
    return NULL;   //都找到底了还没有，那就是真没有了
}

Node findMax(Node root){   //查找最大值就更简单了，最右边的一定是最大的
    while (root && root->right) 
        root = root->right;
    return root;
}

我们来尝试查找一下：

int main() {
    Node root = insert(NULL, 18);   //插入后，得到根结点
    insert(root, 10);
    insert(root, 20);
    insert(root, 7);
    insert(root, 15);
    insert(root, 22);
    insert(root, 9);

    printf("%p\n", find(root, 17));
    printf("%p\n", find(root, 9));
}

搜索17的结果为NULL，说明没有这个结点，而9则成功找到了。

最后我们来看看二叉查找树的删除操作，这个操作就比较麻烦了，因为可能会出现下面的几种情况：

要删除的结点是叶子结点。
要删除的结点是只有一个孩子结点。
要删除的结点有两个孩子结点。

首先我们来看第一种情况，这种情况实际上最好办，直接删除就完事了：

而第二种情况，就有点麻烦了，因为有一个孩子，就像一个拖油瓶一样，你离开了还不行，你还得对他负责才可以。当移除后，需要将孩子结点连接上去：

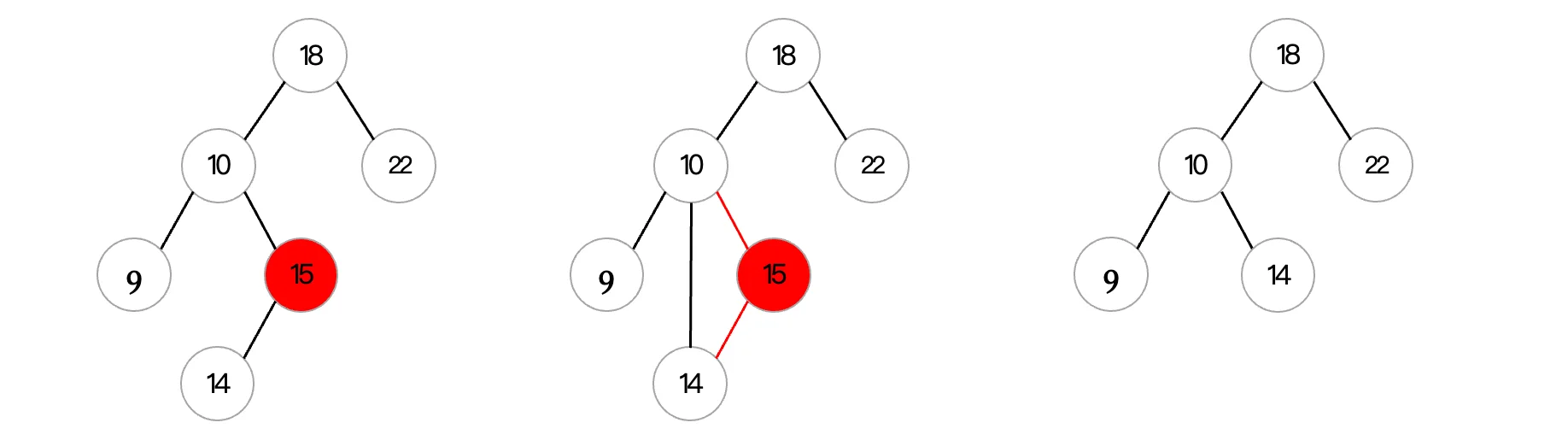
可以看到在调整后，依然满足二叉查找树的性质。最后是最麻烦的有两个孩子的情况，这种该怎么办呢？前面只有一个孩子直接上位就完事，但是现在两个孩子，到底谁上位呢？这就不好办了，为了保持二叉查找树的性质，现在有两种选择：

选取其左子树中最大结点上位
选择其右子树中最小结点上位

这里我们以第一种方式为例：

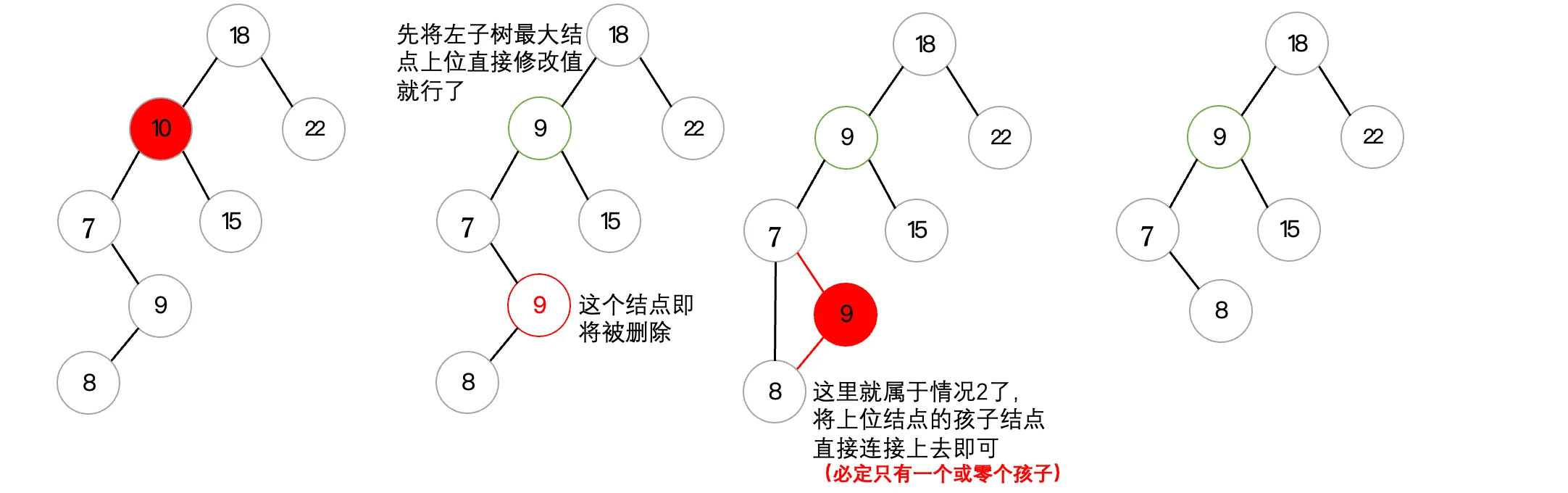
现在我们已经分析完三种情况了，那么我们就来编写一下代码吧：

Node delete(Node root, E target){
    if(root == NULL) return NULL;   //都走到底了还是没有找到要删除的结点，说明没有，直接返回空
    if(root->element > target)   //这里的判断跟之前插入是一样的，继续往后找就完事，直到找到为止
        root->left = delete(root->left, target);
    else if(root->element < target)
        root->right = delete(root->right, target);
    else {   //这种情况就是找到了
        if(root->left && root->right) {   //先处理最麻烦的左右孩子都有的情况
            Node max = findMax(root->left);  //寻找左子树中最大的元素
            root->element = max->element;  //找到后将值替换
            root->left = delete(root->left, root->element);  //替换好后，以同样的方式去删除那个替换上来的结点
        } else {   //其他两种情况可以一起处理，只需要删除这个结点就行，然后将root指定为其中一个孩子，最后返回就完事
            Node tmp = root;
            if(root->right) {   //不是左边就是右边
                root = root->right;
            } else {
                root = root->left;
            }
            free(tmp);   //开删
        }
    }
    return root;   //返回最终的结点
}

这样，我们就完成了二叉查找树的各种操作，当然目前为止我们了解的二叉树高级结构还比较简单，后面就开始慢慢复杂起来了。

二叉搜索树（Binary Search Tree, BST） ​

二叉搜索树（Binary Search Tree, BST）