队列(Queue)

队列是一种特殊的受限制的线性表。

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出的t（First In First Out）的线性表，简称FIFO。允许插入的一端为队尾，允许删除的一端为队头。队列不允许在中间部位进行操作！假设队列是q=（a1，a2，……，an），那么a1就是队头元素，而an是队尾元素。这样我们就可以删除时，总是从a1开始，而插入时，总是在队列最后。这也比较符合我们通常生活中的习惯，排在第一个的优先出列，最后来的当然排在队伍最后。如下图：

前面我们学习了栈，栈中元素只能栈顶出入，它是一种特殊的线性表，同样的，队列（Queue）也是一种特殊的线性表。

就像我们在超市、食堂需要排队一样，我们总是排成一列，先到的人就排在前面，后来的人就排在后面，越前面的人越先完成任务，这就是队列，队列有队头和队尾：

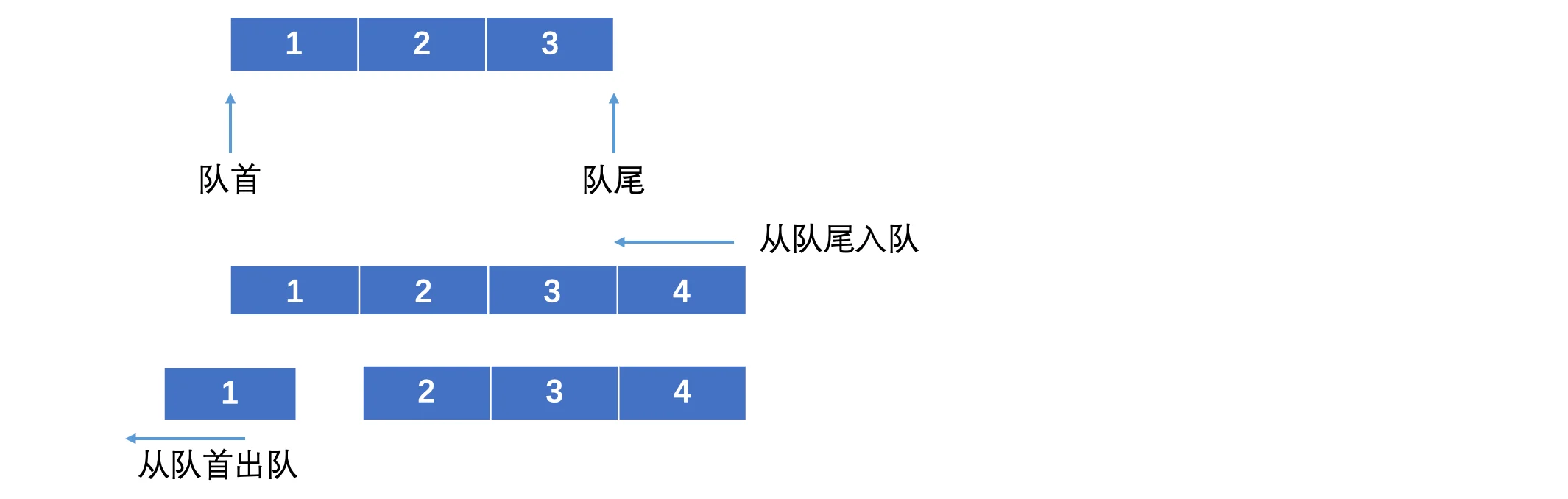
秉承先来后到的原则，队列中的元素只能从队尾进入，只能从队首出去，也就是说，入队顺序为1、2、3、4，那么出队顺序也一定是1、2、3、4，所以队列是一种先进先出（FIFO，First In, First Out）的数据结构。

想要实现队列也是很简单的，也可以通过两种线性表来实现，我们先来看看使用顺序表如何实现队列，假设一开始的时候队列中有0个元素，队首和队尾一般都初始都是-1这个位置：

此时有新的元素入队了，队尾向后移动一格（+1），然后在所指向位置插入新的元素：

之后都是同样的方式进行插入，队尾会一直向后移动：

现在我们想要执行出队操作了，那么需要将队首向后移动一格，然后删除队首指向的元素：

看起来设计的还挺不错的，不过这样有一个问题，这个队列是一次性的，如果队列经过反复出队入队操作，那么最后指针会直接指向数组的最后，如果我们延长数组的话，也不是一个办法，不可能无限制的延伸下去吧？所以一般我们采用循环队列的形式，来实现重复使用一个数组（不过就没办法扩容了，大小是固定的）

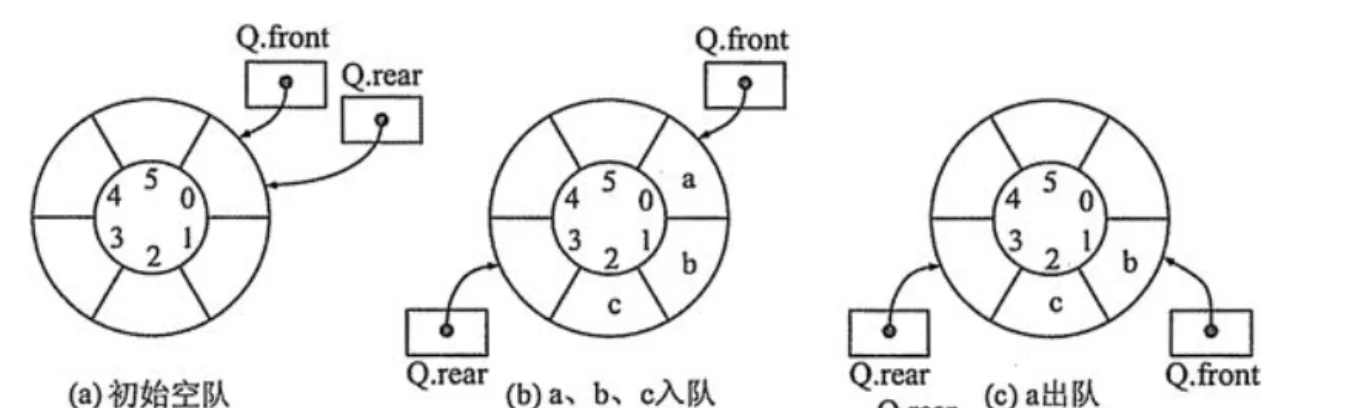
我们可以在移动队首队尾指针时，考虑循环的问题，也就是说如果到达了数组尽头，那么就直接从数组的前面重新开始计算，这样就相当于逻辑上都循环了，队首和队尾指针在一开始的时候都指向同一个位置，每入队一个新的元素，依然是先让队尾后移一位，在所指向位置插入元素，出队同理。

不过这样还是有问题，既然是循环的，那么怎么判断队列是否已满呢？

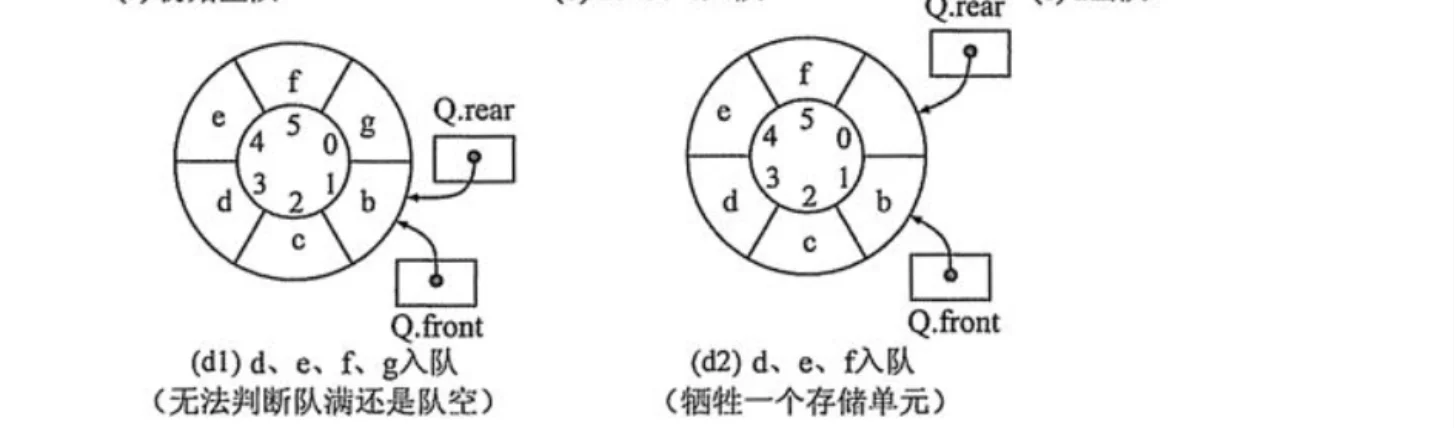
由于队首指针和队尾指针重合时表示队列为空，所以我们只能舍弃一个存储单元，当队尾距离队首一个单元的时候，表示队列已满。

好了，现在理论讲解完毕，我们可以开始编写代码了：

typedef int E;

struct Queue {
    E * array;
    int capacity;   //数组容量
    int rear, front;   //队尾、队首指针
};

typedef struct Queue * ArrayQueue;

接着我们来对其进行初始化：

_Bool initQueue(ArrayQueue queue){
    queue->array = malloc(sizeof(E) * 10);
    if(queue->array == NULL) return 0;
    queue->capacity = 10;
    queue->front = queue->rear = 0;   //默认情况下队首和队尾都指向0的位置
    return 1;
}

int main(){
    struct Queue queue;
    initQueue(&queue);   
}

接着我们来编写一下入队操作：

_Bool offerQueue(ArrayQueue queue, E element){
    if((queue->rear + 1) % queue->capacity == queue->front)   //先判断队列是否已满，如果队尾下一个就是队首，那么说明已满
        return 0;
    queue->rear = (queue->rear + 1) % queue->capacity;   //队尾先向前移动一位，注意取余计算才能实现循环
    queue->array[queue->rear] = element;   //在新的位置插入元素
    return 1;
}

我们来测试一下：

void printQueue(ArrayQueue queue){
    printf("<<< ");
    int i = queue->front;   //遍历队列需要从队首开始
    do {
        i = (i + 1) % queue->capacity;   //先向后循环移动
        printf("%d ", queue->array[i]);  //然后打印当前位置上的元素
    } while (i != queue->rear);   //当到达队尾时，结束
    printf("<<<\n");
}

int main(){
    struct Queue queue;
    initQueue(&queue);
    for (int i = 0; i < 5; ++i) {
        offerQueue(&queue, i * 100);
    }
    printQueue(&queue);
}

最后结果如下：

我们接着来看出队操作：

_Bool isEmpty(ArrayQueue queue){   //在出队之前需要先看看容量是否足够
    return queue->rear == queue->front;
}

E pollQueue(ArrayQueue queue){
    queue->front = (queue->front + 1) % queue->capacity;   //先将队首指针后移
    return queue->array[queue->front];   //出队，完事
}

我们来测试一下吧：

int main(){
    struct Queue queue;
    initQueue(&queue);
    for (int i = 0; i < 5; ++i) {
        offerQueue(&queue, i * 100);
    }
    printQueue(&queue);
    while (!isEmpty(&queue)) {
        printf("%d ", pollQueue(&queue));
    }
}

我们来看看结果：

可以看到，队列是先进先出的，我们是以什么顺序放入队列中，那么出来的就是是什么顺序。

同样的，队列也可以使用链表来实现，并且使用链表的话就不需要关心容量之类的问题了，会更加灵活一些：

注意我们需要同时保存队首和队尾两个指针，因为是单链表，所以队首需要存放指向头结点的指针，因为需要的是前驱结点，而队尾则直接是指向尾结点的指针即可，后面只需要直接在后面拼接就行。

当有新的元素入队时，只需要拼在队尾就行了，同时队尾指针也要后移一位：

出队时，只需要移除队首指向的下一个元素即可：

那么我们就按照这个思路，来编写一下代码吧：

typedef int E;

struct LNode {
    E element;
    struct LNode * next;
};

typedef struct LNode * Node;

struct Queue{
    Node front, rear;
};

typedef struct Queue * LinkedQueue;   //因为要存储首位两个指针，所以这里封装一个新的结构体吧

接着是初始化，初始化的时候，需要把头结点先创建出来：

_Bool initQueue(LinkedQueue queue){
    Node node = malloc(sizeof(struct LNode));
    if(node == NULL) return 0;
    node->next = NULL;
    queue->front = queue->rear = node;   //一开始两个指针都是指向头结点的，表示队列为空
    return 1;
}

int main(){
    struct Queue queue;
    initQueue(&queue);
}

首先是入队操作，入队其实直接在后面插入新的结点就行了：

_Bool offerQueue(LinkedQueue queue, E element){
    Node node = malloc(sizeof(struct LNode));
    if(node == NULL) return 0;
    node->next = NULL;
    node->element = element;
    queue->rear->next = node;   //先让尾结点的下一个指向新的结点
    queue->rear = node;   //然后让队尾指针指向新的尾结点
    return 1;
}

我们来测试一下看看：

void printQueue(LinkedQueue queue){
    printf("<<< ");
    Node node = queue->front->next;
    while (1) {    //注意不能直接判空，因为前面我们没考虑，也就没将新结点next设定为NULL
        printf("%d ", node->element);
        if(node == queue->rear) break;    //当已经打印最后一个元素后，再结束
        else node = node->next;
    }
    printf("<<<\n");
}

int main(){
    struct Queue queue;
    initQueue(&queue);
    for (int i = 0; i < 5; ++i) {
        offerQueue(&queue, i*100);
    }
    printQueue(&queue);
}

测试结果如下：

接着是出队操作，出队操作要相对麻烦一点：

E pollQueue(LinkedQueue queue){
    E e = queue->front->next->element;
    Node node = queue->front->next;
    queue->front->next = queue->front->next->next;  //直接让头结点指向下下个结点
    if(queue->rear == node) queue->rear = queue->front;   //如果队尾就是待出队的结点，那么队尾回到队首位置上
    free(node);   //释放内存
    return e;
}

这样，我们就编写好了：

int main(){
    struct Queue queue;
    initQueue(&queue);
    for (int i = 0; i < 5; ++i) {
        offerQueue(&queue, i*100);
    }
    printQueue(&queue);
    while (!isEmpty(&queue)){
        printf("%d ", pollQueue(&queue));
    }
}

测试结果如下：

效果和前面的数组实现是一样的，只不过使用链表会更加灵活一些。

队列练习题：

使用链表方式存储的队列，在进行出队操作时需要？
A. 仅修改头结点指向 B. 仅修改尾指针 C. 头结点指向、尾指针都要修改 D. 头结点指向、尾指针可能都要修改
首先出队肯定是要动头结点指向的，但是不一定需要动尾指针，因为只有当尾指针指向的是待出队的元素时才需要，因为执行后队列就为空了，所以需要将队尾指针移回头结点处，选择D
引起循环队列队头位置发生变化的操作是？
A. 出队
B. 入队
C. 获取队头元素
D. 获取队尾元素
这个题还是很简单的，因为只有出队操作才会使得队头位置后移，所以选择A

队列(Queue) ​

队列(Queue)