排序算法
基本概念
现实生活中排序很重要,例如:淘宝按条件搜索的结果展示等。
概念
排序是计算机内经常进行的一种操作,其目的是将一组“无序”的数据元素调整为“有序”的数据元素。
排序数学定义:
假设含n个数据元素的序列为{R1, R2, …, Rn},其相应的关键字序列为{K1, K2, …, Kn},这些关键字相互之间可以进行比较,即在它们之间存在着这样一个关系 :Kp1 ≤ Kp2 ≤ … ≤ Kpn
按此固有关系将上式记录序列重新排列为{Rp1, Rp2, …,Rpn}的操作称作排序
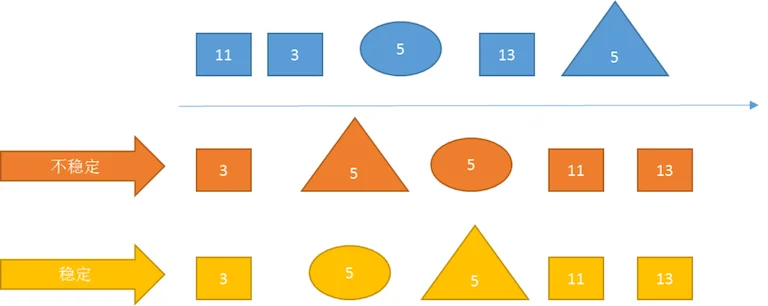
排序的稳定性
如果在序列中有两个数据元素r[i]和r[j],它们的关键字k[i] == k[j],且在排序之前,对象r[i]排在r[j]前面。如果在排序之后,对象r[i]仍在r[j]前面,则称这个排序方法是稳定的,否则称这个排序方法是不稳定的。
多关键字排序
排序时需要比较的关键字多余一个,排序结果首先按关键字1进行排序,当关键字1相同时按关键字2进行排序,当关键字n-1相同时按关键字n进行排序,对于多关键字排序,只需要在比较操作时同时考虑多个关键字即可!
排序中的关键操作
比较:任意两个数据元素通过比较操作确定先后次序。
交换:数据元素之间需要交换才能得到预期结果。
内排序和外排序
内排序:在排序过程中,待排序的所有记录全部都放置在内存中,排序分为:内排序和外排序。
外排序:由于排序的记录个数太多,不能同时放置在内存,整个排序过程需要在内外存之间多次交换数据才能进行。
排序的审判
时间性能:关键性能差异体现在比较和交换的数量
辅助存储空间:为完成排序操作需要的额外的存储空间,必要时可以“空间换时间”
算法的实现复杂性:过于复杂的排序法会影响代码的可读性和可维护性,也可能影响排序的性能
总结
排序是数据元素从无序到有序的过程
排序具有稳定性,是选择排序算法的因素之一
比较和交换是排序的基本操作
多关键字排序与单关键字排序无本质区别
排序的时间性能是区分排序算法好坏的主要因素
选择排序
算法介绍
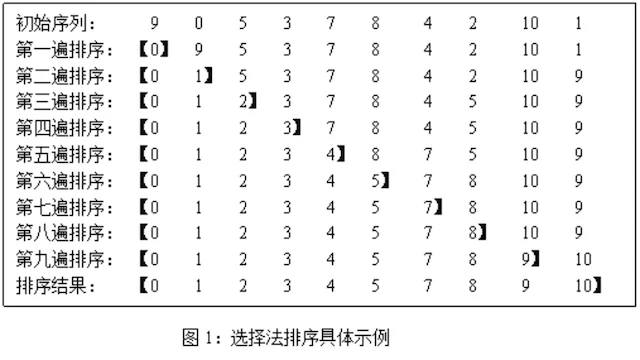
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
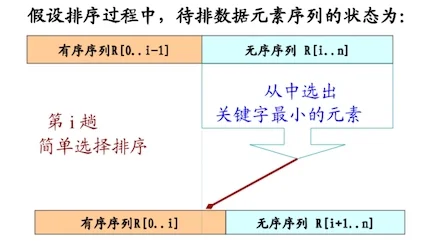
基本思想
设数组为a[0…n-1]。
初始时,数组全为无序区为
a[0..n-1]。令i=0在无序区
a[i…n-1]中选取一个最小的元素,将其与a[i]交换。交换之后a[0…i]就形成了一个有序区。i++并重复第二步直到i==n-1。排序完成。
稳定性
选择排序是不稳定的排序方法
选择排序效率:O(n²)
排序过程

算法实现

冒泡排序
算法介绍
冒泡排序算法的运作如下:(从后往前)
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
基本思想
设数组长度为N。
比较相邻的前后两个数据,如果前面数据大于后面的数据,就将二个数据交换。
这样对数组的第0个数据到N-1个数据进行一次遍历后,最大的一个数据就“升”到数组第N-1个位置。
N=N-1,如果N不为0就重复前面二步,否则排序完成。
稳定性
冒泡排序是一种稳定的排序算法
冒泡排序的效率:O(n²)
排序过程

算法实现


冒泡总结:
冒泡排序是一种效率低下的排序方法,在数据规模很小时,可以采用。数据规模比较大时,最好用其它排序方法。
上述例子中对冒泡做了优化,添加了exchange作为标记,记录序列是否已经有序,减少循环次数。
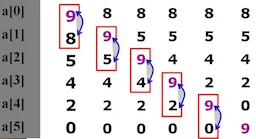
- 上述例子总对冒泡做了优化,添加了flag作为标记,记录序列是否已经有序,减少循环次数。
插入排序
插入排序算法是一种简单的排序算法,也称为。它是一种稳定的排序算法,对局部有序的数据具有较高的效率。
插入排序算法是一个队少量元素进行排序的有效算法。比如,打牌是我们使用插入排序方法最多的日常生活例子。我们在摸牌时,一般会重复一下步骤。期初,我们手里没有牌,摸出第一张,随意放在左手上,以后每一次摸排,都会按照花色从小到大排列,直到所有的牌摸完。插入排序算法采用的类似思路,每一次从无序序列中拿出一个数据,将它放到已排序的序序列的正确位置,如此重复,直到所有的无序序列中的数据都找到了正确位置。
算法介绍
每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子序列中的适当位置,直到全部记录插入完成为止。
基本思想
设数组为a[0…n-1]。
初始时,
a[0]自成1个有序区,无序区为a[1..n-1]。令i=1将
a[i]并入当前的有序区a[0…i-1]中形成a[0…i]的有序区间。i++并重复第二步直到i==n-1。排序完成。
稳定性
插入排序是稳定的排序算法
插入排序效率:O(n²)
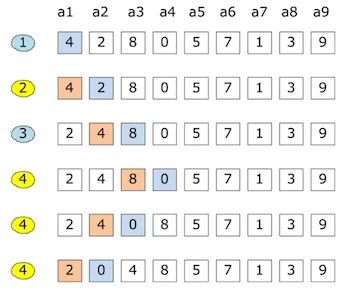
排序过程

算法实现

希尔排序
算法介绍
希尔排序的实质就是分组插入排序,该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
基本思想
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前三种方法有较大提高。
稳定性
希尔排序是不稳定的排序算法。
希尔排序的效率:O(n*logn)≈ O(1.3*n)
排序过程

算法实现

关于希尔排序步长的说明
步长的计算公式可以自行制定,最后步长 == 1即可。
通过大量测试得出的结论:步长 = 步长 / 3 + 1
快速排序
算法介绍
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
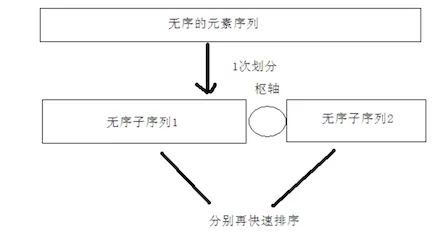
分治法基本思想
先从数列中取出一个数作为基准数(枢轴)。
分区过程将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
再对左右区间重复第二步,直到各区间只有一个数。
稳定性
快速排序是一种不稳定的排序算法。
排序效率: O(N*logN)
排序过程


算法实现


归并排序
算法介绍
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
基本思想
基本思路就是将数组分成二组A,B,如果这二组组内的数据都是有序的,那么就可以很方便的将这二组数据进行排序。如何让这二组组内数据有序了?
可以将A,B组各自再分成二组。依次类推,当分出来的小组只有一个数据时,可以认为这个小组组内已经达到了有序,然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列,再合并数列就完成了归并排序。
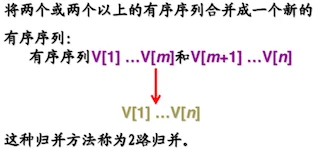
归并的定义

稳定性
归并排序是一种稳定的排序算法。
排序效率: O(N*logN)
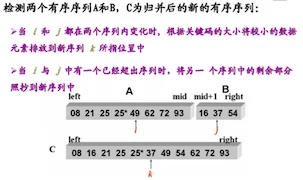
如何合并连个有序序列???
只要从比较二个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。
图例分析
- 代码实现


排序过程

算法实现

堆排序
二叉堆
- 定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。
当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。
下图展示一个最小堆:
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就
简称为堆。
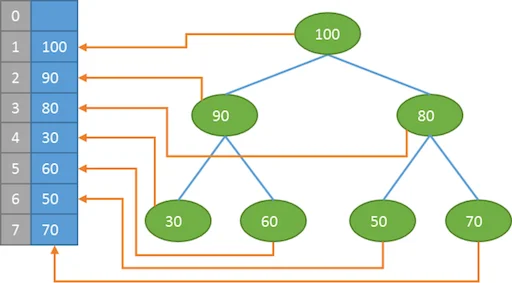
堆的存储
一般都用数组来表示堆,从数组的1号位置开始存储树的根节点,i结点的父结点下标就为i / 2。它的左右子结点下标分别为2 * i 和2 * i + 1。如第1个结点左右子结点下标分别为2和3。数组的零号位置一般空闲不用。
堆的插入(向上渗透)
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列,现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中
堆的删除(向下渗透)
按定义,堆中每次都只能删除第0个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。
总结
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 平均空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 选择排序 | O(n²) | O(n²) | O(1) | 不稳定 |
| 冒泡排序 | O(n²) | O(n²) | O(1) | 稳定 |
| 直接插入排序 | O(n²) | O(n²) | O(1) | 稳定 |
| 希尔排序 | O(nlogn) | O(n²) | O(log₂n) | 不稳定 |
| 快速排序 | O(nlogn) | O(n²) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(1) | 不稳定 |