自平衡二叉搜索树（AVL Tree）

前面我们介绍了二叉查找树，利用二叉查找树，我们在搜索某个值的时候，效率会得到巨大提升。但是虽然看起来比较完美，也是存在缺陷的，比如现在我们依次将下面的值插入到这棵二叉树中：

20 15 13 8 6 3

在插入完成后，我们会发现这棵二叉树竟然长这样：

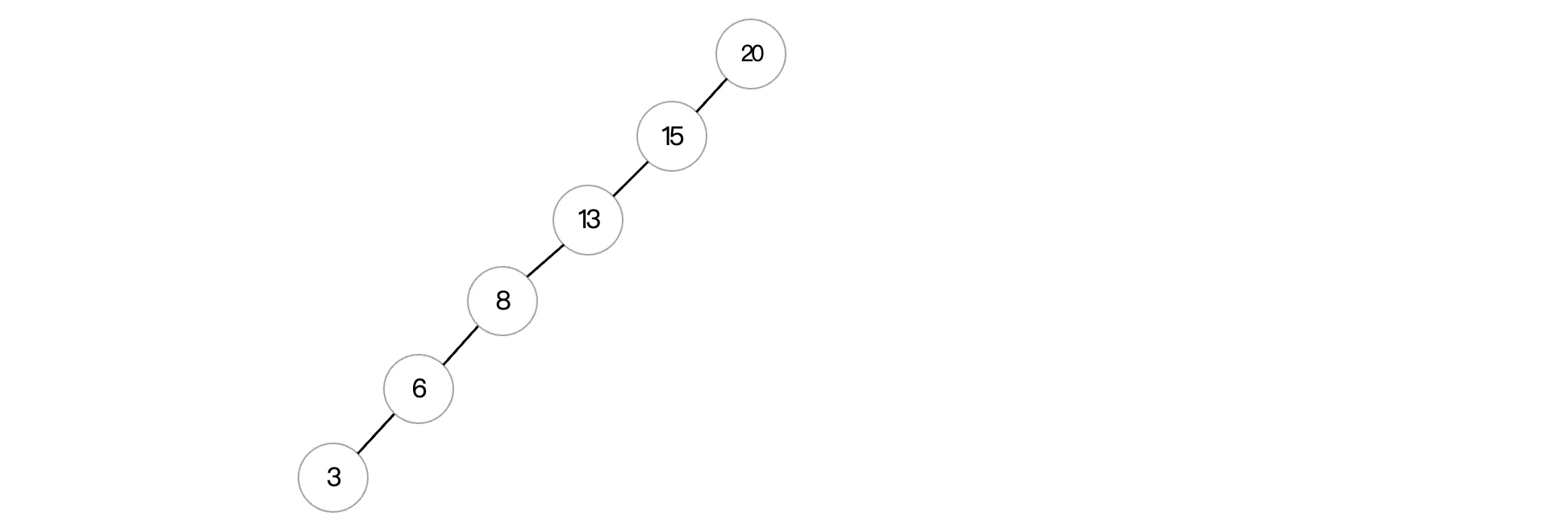
因为根据我们之前编写的插入规则，小的一律往左边放，现在正好来的就是这样一串递减的数字，最后就组成了这样的一棵只有一边的二叉树，这种情况，与其说它是一棵二叉树，不如说就是一个链表，如果这时我们想要查找某个结点，那么实际上查找的时间并没有得到任何优化，直接就退化成线性查找了。

所以，二叉查找树只有在理想情况下，查找效率才是最高的，而像这种极端情况，就性能而言几乎没有任何的提升。我们理想情况下，这样的效率是最高的：

所以，我们在进行结点插入时，需要尽可能地避免这种一边倒的情况，这里就需要引入平衡二叉树的概念了。实际上我们发现，在插入时如果不去维护二叉树的平衡，某一边只会无限制地延伸下去，出现极度不平衡的情况，而我们理想中的二叉查找树左右是尽可能保持平衡的，平衡二叉树（AVL树）就是为了解决这样的问题而生的。

它的性质如下：

平衡二叉树一定是一棵二叉查找树。
任意结点的左右子树也是一棵平衡二叉树。
从根节点开始，左右子树都高度差不能超过1，否则视为不平衡。

可以看到，这些性质规定了平衡二叉树需要保持高度平衡，这样我们的查找效率才不会因为数据的插入而出现降低的情况。二叉树上节点的左子树高度减去右子树高度，得到的结果称为该节点的平衡因子（Balance Factor），比如：

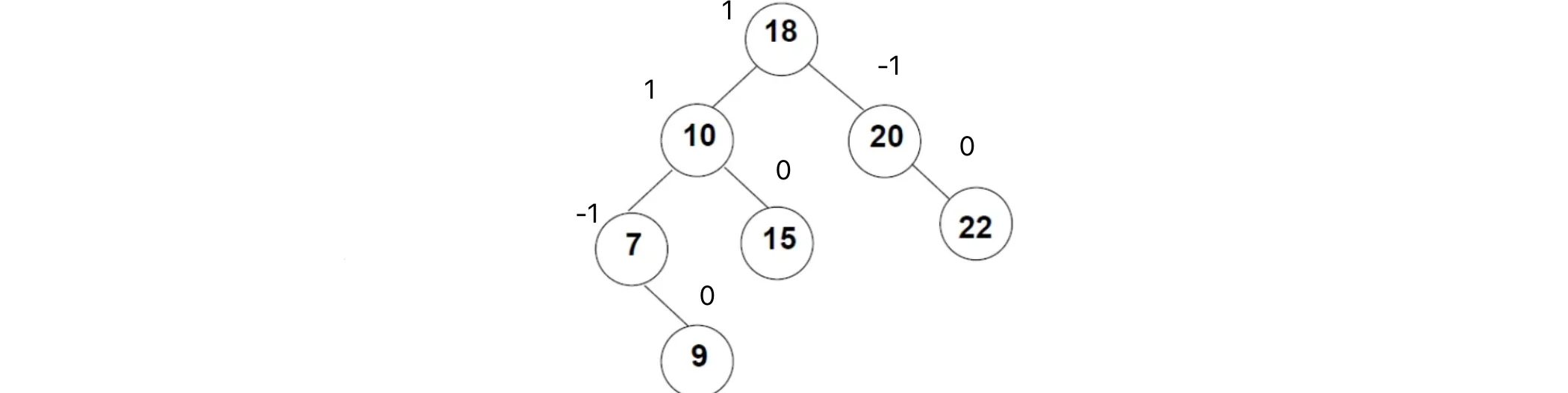
通过计算平衡因子，我们就可以快速得到是否出现失衡的情况。比如下面的这棵二叉树，正在执行插入操作：

可以看到，当插入之后，不再满足平衡二叉树的定义时，就出现了失衡的情况，而对于这种失衡情况，为了继续保持平衡状态，我们就需要进行处理了。我们可能会遇到以下几种情况导致失衡：

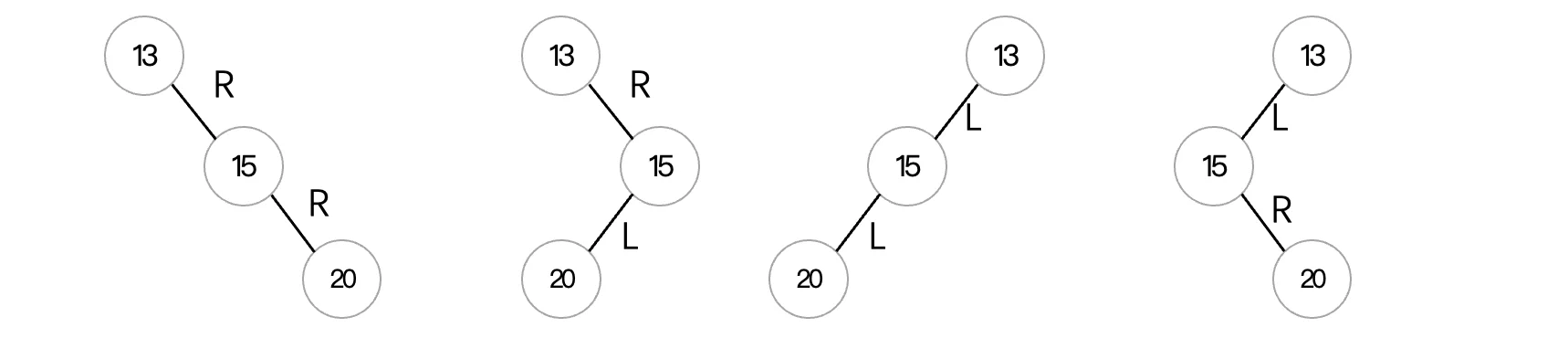
根据插入结点的不同偏向情况，分为LL型、LR型、RR型、RL型。针对于上面这几种情况，我们依次来看一下如何进行调整，使得这棵二叉树能够继续保持平衡：

动画网站：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html（实在不理解可以看看动画是怎么走的）

LL型调整（右旋）
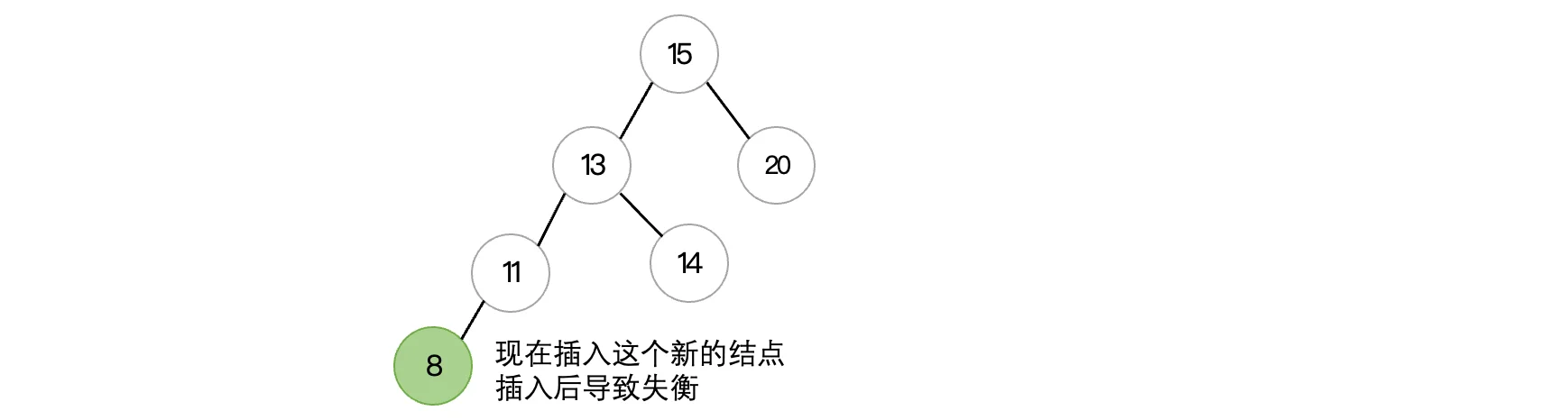
首先我们来看这种情况，这是典型的LL型失衡，为了能够保证二叉树的平衡，我们需要将其进行旋转来维持平衡，去纠正最小不平衡子树即可。那么怎么进行旋转呢？对于LL型失衡，我们只需要进行右旋操作，首先我们先找到最小不平衡子树，注意是最小的那一个：
可以看到根结点的平衡因子是2，是目前最小的出现不平衡的点，所以说从根结点开始向左的三个结点需要进行右旋操作，右旋需要将这三个结点中间的结点作为新的根结点，而其他两个结点现在变成左右子树：
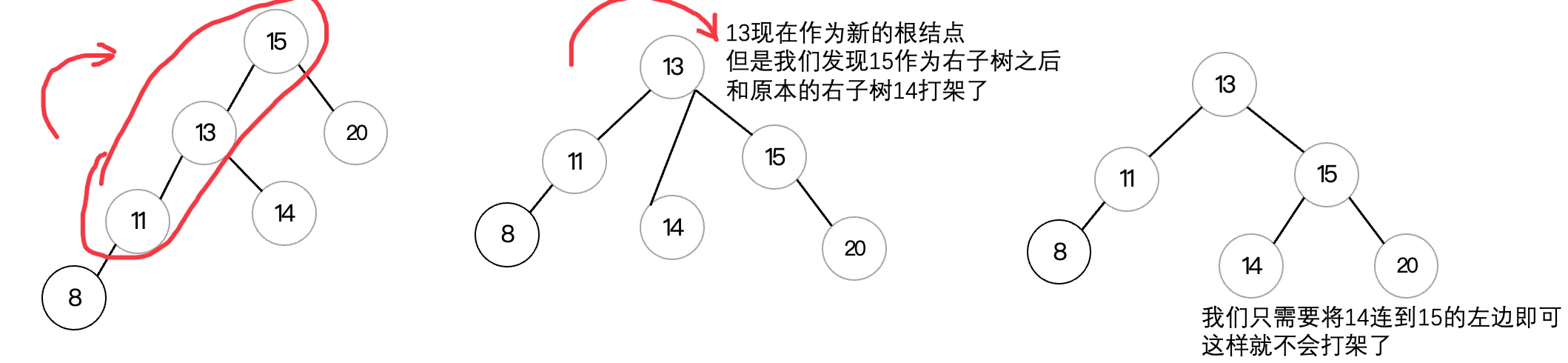
这样，我们就完成了右旋操作，可以看到右旋之后，所有的结点继续保持平衡，并且依然是一棵二叉查找树。
RR型调整（左旋）
前面我们介绍了LL型以及右旋解决方案，相反的，当遇到RR型时，我们只需要进行左旋操作即可：
操作和上面是一样的，只不过现在反过来了而已：
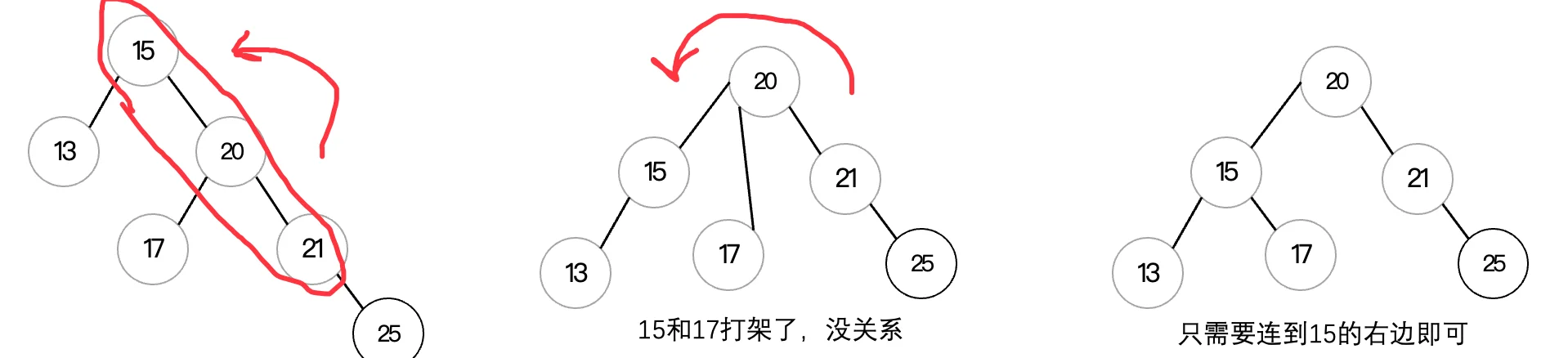
这样，我们就完成了左旋操作，使得这棵二叉树继续保持平衡状态了。
RL型调整（先右旋，再左旋）
剩下两种类型比较麻烦，需要旋转两次才行。我们来看看RL型长啥样：
可以看到现在的形状是一个回旋镖形状的，先右后左的一个状态，也就是RL型，针对于这种情况，我们需要先进行右旋操作，注意这里的右旋操作针对的是后两个结点：
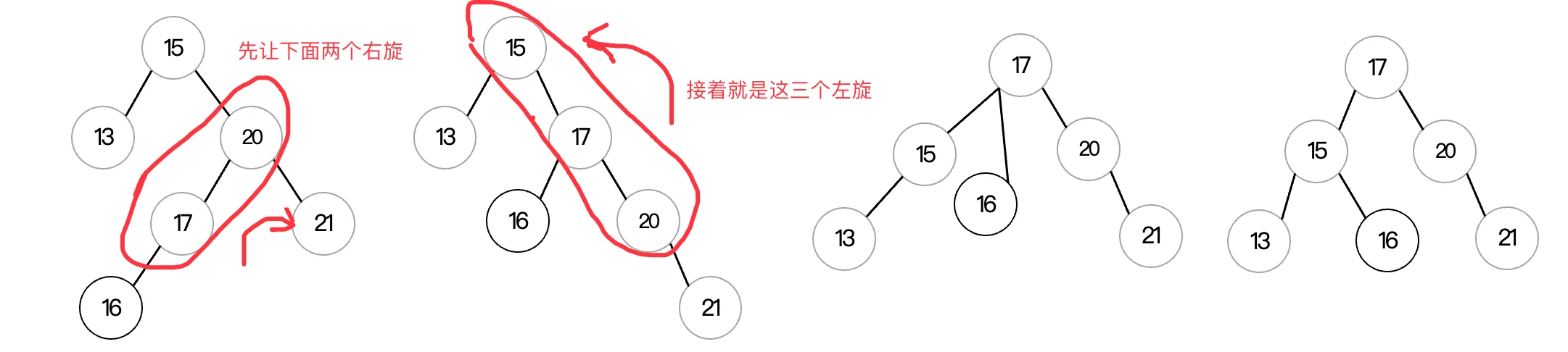
其中右旋和左旋的操作，与之前一样，该怎么分配左右子树就怎么分配，完成两次旋转后，可以看到二叉树重新变回了平衡状态。
LR型调整（先左旋，再右旋）
和上面一样，我们来看看LR型长啥样，其实就是反着的：
形状是先向左再向右，这就是典型的LR型了，我们同样需要对其进行两次旋转：
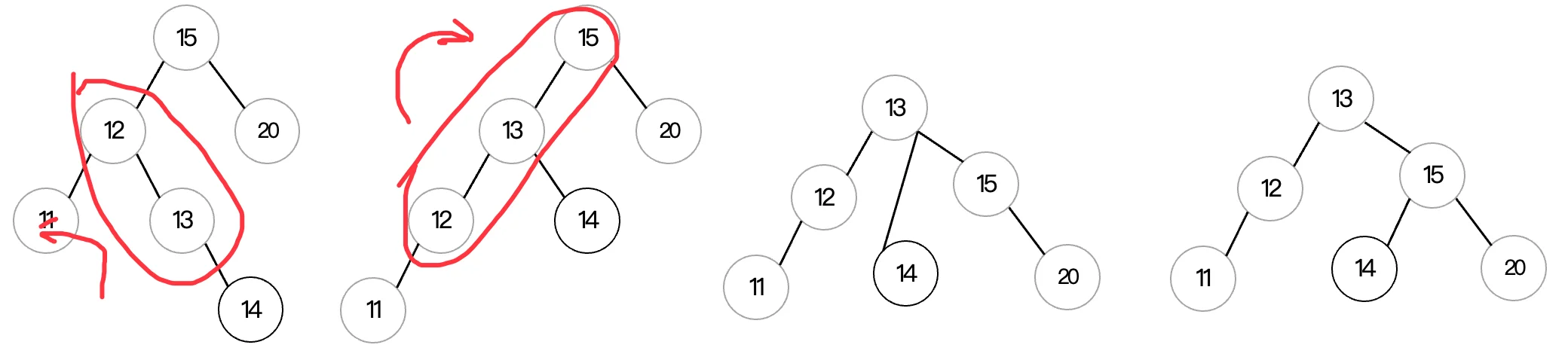
这里我们先进行的是左旋，然后再进行的右旋，这样二叉树就能继续保持平衡了。

这样，我们只需要在插入结点时注意维护整棵树的平衡因子，保证其处于稳定状态，这样就可以让这棵树一直处于高度平衡的状态，不会再退化了。这里我们就编写一个插入结点代码来实现一下吧，首先还是结点定义：

typedef int E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int height;   //每个结点需要记录当前子树的高度，便于计算平衡因子
} * Node;

Node createNode(E element){
    Node node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    node->height = 1;   //初始化时，高度写为1就可以了
    return node;
}

接着我们需要先将左旋、右旋等操作编写出来，因为一会插入时可能需要用到：

int max(int a, int b){
    return a > b ? a : b;
}

int getHeight(Node root){
    if(root == NULL) return 0;
    return root->height;
}

Node leftRotation(Node root){  //左旋操作，实际上就是把左边结点拿上来
    Node newRoot = root->right;   //先得到左边结点
    root->right = newRoot->left;   //将左边结点的左子树丢到原本根结点的右边去
    newRoot->left = root;   //现在新的根结点左边就是原本的跟结点了

    root->height = max(getHeight(root->right), getHeight(root->left)) + 1;
    newRoot->height = max(getHeight(newRoot->right), getHeight(newRoot->left)) + 1;
    return newRoot;
}

Node rightRotation(Node root){
    Node newRoot = root->left;
    root->left = newRoot->right;
    newRoot->right = root;

    root->height = max(getHeight(root->right), getHeight(root->left)) + 1;
    newRoot->height = max(getHeight(newRoot->right), getHeight(newRoot->left)) + 1;
    return newRoot;
}

Node leftRightRotation(Node root){
    root->left = leftRotation(root->left);
    return rightRotation(root);
}

Node rightLeftRightRotation(Node root){
    root->right = rightRotation(root->right);
    return leftRotation(root);
}

最后就是我们的插入操作了，注意在插入时动态计算树的高度，一旦发现不平衡，那么就立即采取对应措施：

Node insert(Node root, E element){
    if(root == NULL) {    //如果结点为NULL，说明找到了插入位置，直接创建新的就完事
        root = createNode(element);
    }else if(root->element > element) {   //和二叉搜索树一样，判断大小，该走哪边走哪边，直到找到对应插入位置
        root->left = insert(root->left, element);
        if(getHeight(root->left) - getHeight(root->right) > 1) {   //插入完成之后，需要计算平衡因子，看看是否失衡
            if(root->left->element > element) //接着需要判断一下是插入了左子树的左边还是右边，如果是左边那边说明是LL，如果是右边那说明是LR
                root = rightRotation(root);   //LL型得到左旋之后的结果，得到新的根结点
            else
                root = leftRightRotation(root);    //LR型得到先左旋再右旋之后的结果，得到新的根结点
        }
    }else if(root->element < element){
        root->right = insert(root->right, element);
        if(getHeight(root->left) - getHeight(root->right) < -1){
            if(root->right->element < element)
                root = leftRotation(root);
            else
                root = rightLeftRightRotation(root);
        }
    }
    //前面的操作完成之后记得更新一下树高度
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    return root;  //最后返回root到上一级
}

这样，我们就完成了平衡二叉树的插入操作，当然删除操作比较类似，也是需要在删除之后判断是否平衡，如果不平衡同样需要进行旋转操作，这里就不做演示了。

自平衡二叉搜索树（AVL Tree） ​

自平衡二叉搜索树（AVL Tree）