树形结构
基本概念
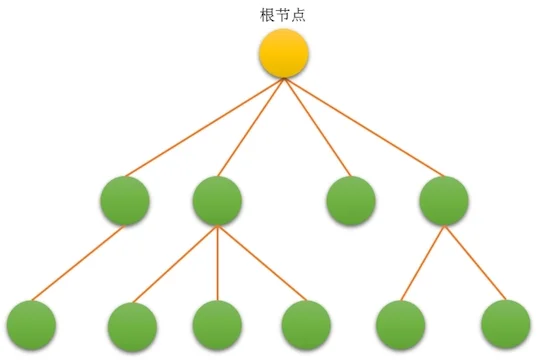
树的定义:
由一个或多个(n≥0)结点组成的有限集合T,有且仅有一个结点称为根(root),当n>1时,其余的结点分为m(m≥0)个互不相交的有限集合T1,T2,…,Tm。每个集合本身又是棵树,被称作这个根的子树 。
树的结构特点
非线性结构,有一个直接前驱,但可能有多个直接后继(1:n)
树的定义具有递归性,树中还有树。
树可以为空,即节点个数为0。
若干术语
- :即根结点(没有前驱)
- :即终端结点(没有后继)
森林:指m棵不相交的树的集合(例如删除A后的子树个数)
有序树:结点各子树从左至右有序,不能互换(左为第一)
无序树:结点各子树可互换位置。
- :即上层的那个结点(直接前驱) parent
- :即下层结点的子树 (直接后继) child
兄弟:同一双亲下的同层结点(孩子之间互称兄弟)sibling
堂兄弟:即双亲位于同一层的结点(但并非同一双亲)cousin
祖先:即从根到该结点所经分支的所有结点
子孙:即该结点下层子树中的任一结点
结点:即树的数据元素
- :结点挂接的子树数(有几个直接后继就是几度)
结点的层次:从根到该结点的层数(根结点算第一层)
终端结点:即度为0的结点,即
分支结点:除树根以外的结点(也称为内部结点)
- :所有结点度中的最大值(Max{各结点的度})
- :指所有结点中最大的层数(Max{各结点的层次})
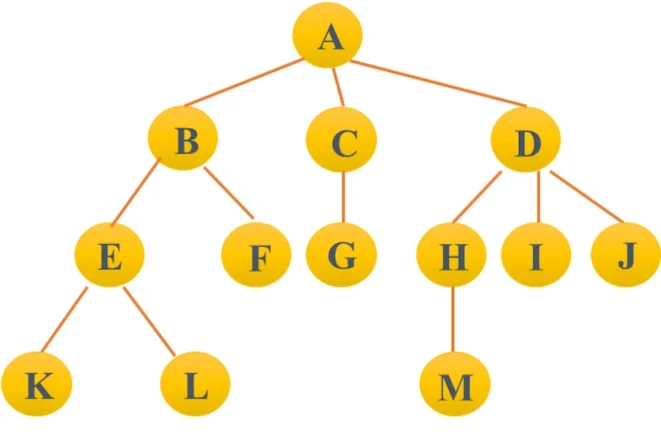
上图中的结点数= 13,树的度= 3,树的深度= 4
- 森林
森林其实很好理解,一片森林肯定是是由很多棵树构成的,比如下面的三棵树:
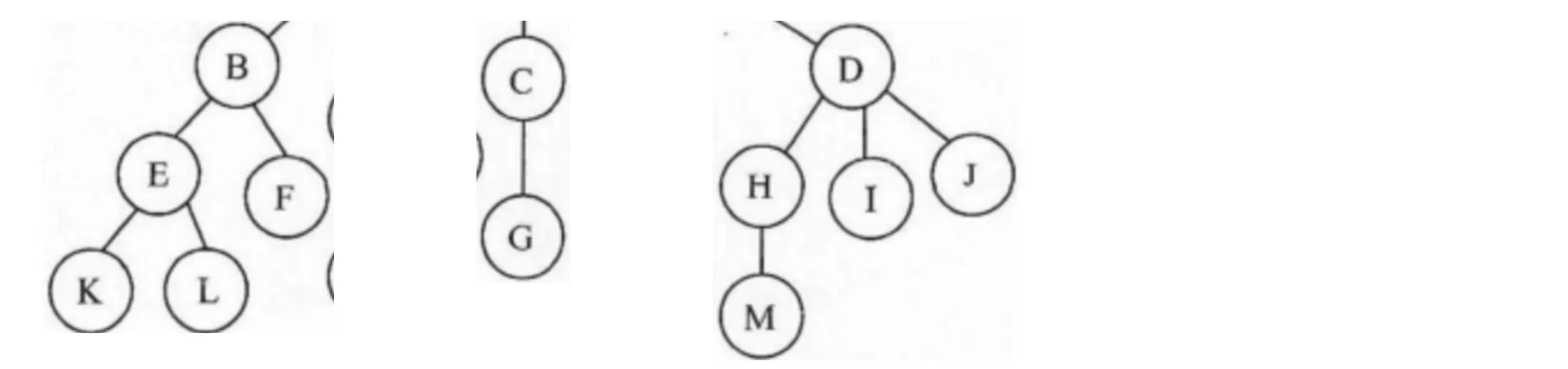
它们共同组成了一片森林,因此,m(m≥0)棵树的集合我们称为森林(Forest)
树的表示法
图形表示法
事物之间的逻辑关系可以通过数的形式很直观的表示出来,如下图:
广义表表示法
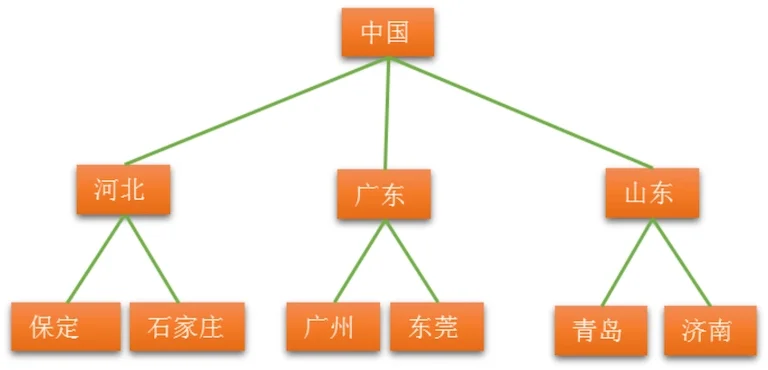
用广义表表示法表示上图:中国(河北(保定,石家庄),广东(广州,东莞),山东(青岛,济南))
根作为由子树森林组成的表的名字写在表的左边。
左孩子右兄弟表示法
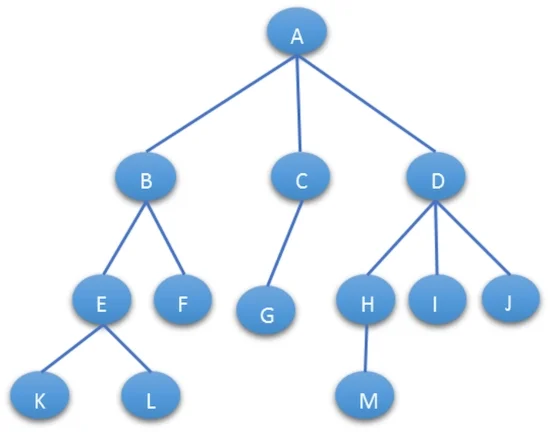
左孩子右兄弟表示法可以将一颗多叉树转化为一颗二叉树:
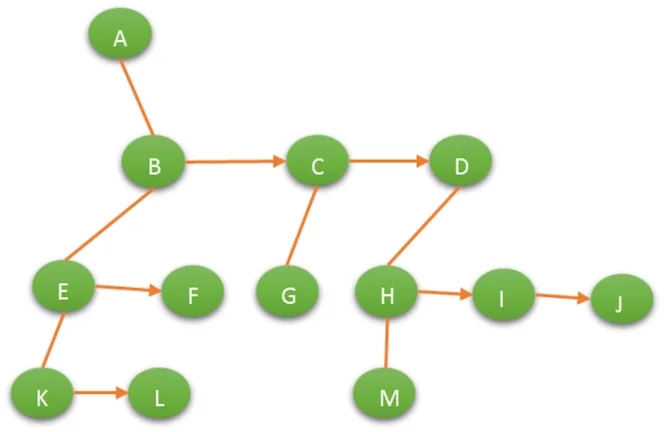
节点的结构:

节点有两个指针域,其中一个指针指向子节点,另一个指针指向其兄弟节点。
常见树形结构
数据结构中的树形结构及其简写表示如下:
二叉树(Binary Tree, BT)
- 每个节点最多有两个子节点(左子树和右子树)。
满二叉树(Full Binary Tree, FBT)
- 所有非叶子节点均有两个子节点,且叶子节点处于同一层。
完全二叉树(Complete Binary Tree, CBT)
- 除最后一层外,其他层节点均满,且最后一层节点从左到右连续填充。
二叉搜索树(Binary Search Tree, BST)
- 左子树所有节点值 < 当前节点值 < 右子树所有节点值。
AVL树(AVL Tree)
- 自平衡二叉搜索树,任意节点左右子树高度差不超过1。
红黑树(Red-Black Tree, RBT)
- 通过颜色标记实现平衡的二叉搜索树,插入和删除效率较高。
B树(B-Tree)
- 多叉平衡树,适合外存存储(如数据库索引),节点可包含多个子节点。
B+树(B+-Tree)
- B树的变种,所有数据存储在叶子节点,支持范围查询和顺序访问。
堆(Heap)
- 分为最大堆(Max-Heap)和最小堆(Min-Heap),用于优先队列,通常基于数组实现。
哈夫曼树(Huffman Tree, HT)
- 带权路径长度最小的二叉树,用于数据压缩和最优编码。
Trie树(Trie Tree, TRIE)
- 前缀树,高效存储和查找字符串,节点按字符分层。
补充说明
- 非线性结构:树形结构以分支关系表达层次化数据,与线性结构(如数组、链表)不同。
- 应用场景:树结构常用于搜索、排序、文件系统、网络路由、数据压缩等领域。